# 五、簡單的前饋神經網絡 神經網絡確實是 Tensorflow 擅長的機器學習領域。 可以用它實現多種類型的架構和算法，以及結合了符號引擎的其他優點，這實際上將有助于訓練更復雜的設置。 在本章中，我們開始利用高表現原語的功能來解決大量支持輸入變量的日益復雜的問題。 在本章中，我們將介紹以下主題： * 神經網絡的初步概念 * 非線性一般函數回歸的神經網絡項目 * 利用非線性回歸預測汽車燃油效率的項目 * 學習葡萄酒的分類和多分類 # 初步概念 為了將簡單的框架構建到神經網絡的組件和架構中，我們將對原始概念進行簡單明了的構建，這些原始概念為當前，復雜而多樣的神經網絡格局鋪平了道路。 ## 人工神經元 人工神經元是一種數學函數，被視為真實生物神經元的模型。 它的主要特征是它接收一個或多個輸入（訓練數據），并對它們求和以產生輸出。 此外，通常對總和進行加權（權重和偏差），然后將總和傳遞給非線性函數（激活函數或傳遞函數）。 ## 原始示例 -- 感知器 感知器是實現人工神經元的最簡單方法之一，并且它的算法可以追溯到 1950 年代，最早是在 1960 年代實現的。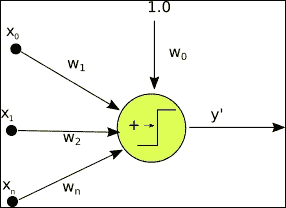 從本質上講，它是一種學習二分類函數的算法，該算法將一個實數映射為兩個數：  下圖顯示了單層感知器 ### 感知機算法 感知器的簡化算法為： 1. 用隨機分布初始化權重（通常為低值） 2. 選擇一個輸入向量并將其呈現給網絡， 3. 為指定的輸入向量和權重值計算網絡的輸出`y'`。 4. 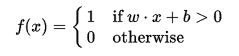用于感知機的函數是：  5. 如果`y' ≠ y`，則通過添加更改`Δw = yx[i]`修改所有連接`w[i]` 6. 返回步驟 2。 ## 神經網絡層 單層感知器可以推廣到彼此連接的多個層，但是仍然存在問題；表示函數是輸入的線性組合，并且感知器只是一種線性分類器，不可能正確擬合非線性函數。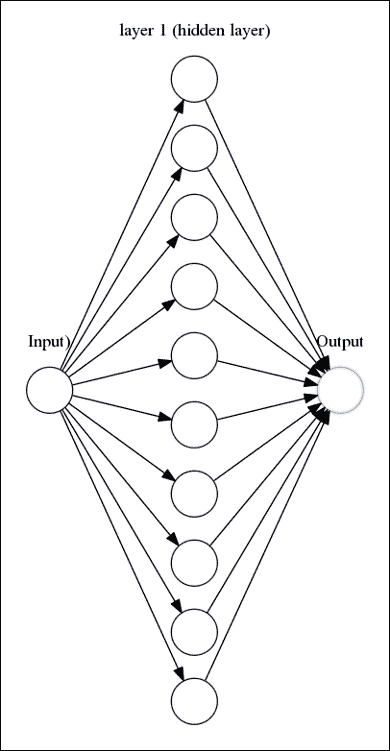  ## 神經網絡激活函數 僅靠單變量線性分類器，神經網絡的學習表現就不會那么好。 甚至機器學習中的一些輕微復雜的問題都涉及多個非線性變量，因此開發了許多變體來替代感知器的傳遞函數。 為了表示非線性模型，可以在激活函數中使用許多不同的非線性函數。 這意味著神經元將對輸入變量的變化做出反應的方式發生變化。 實際上，最常用的激活函數是： * Sigmoid: 規范的激活函數，對于計算分類屬性的概率具有很好的屬性。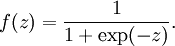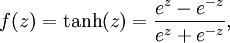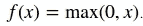  * Tanh: 與 Sigmoid 非常相似，但其值范圍是`[-1,1]`而不是`[0,1]`  * Relu: 這稱為整流線性單元，其主要優點之一是它不受“梯度消失”問題的影響，該問題通常存在于網絡的第一層，趨向于 0 或很小的`epsilon`值：  ## 梯度和反向傳播算法 當我們描述感知器的學習階段時，我們描述了根據權重對最終誤差的“責任”來按比例調整權重的階段。 在這個復雜的神經元網絡中，誤差的責任將分布在整個架構中應用于數據的所有函數之間。 因此，一旦我們計算了總誤差，并且將整個函數應用于原始數據，我們現在就必須嘗試調整方程式中的所有變量以將其最小化。 正如最優化領域所研究的那樣，我們需要知道的是能夠使該誤差最小化的是損失函數的梯度。 鑒于數據要經過許多權重和傳遞函數，因此必須通過鏈式法則來解決合成函數的梯度。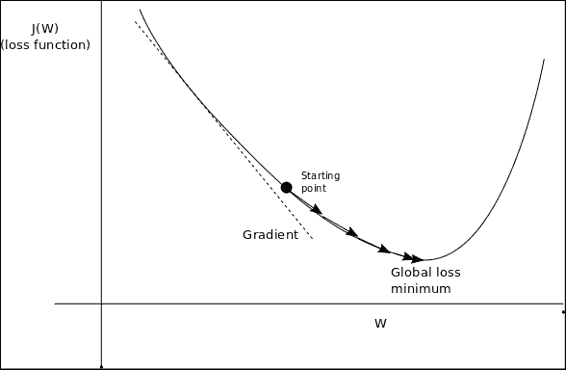 ## 最小化損失函數：梯度下降 讓我們看下圖以了解損失函數：  ### 神經網絡問題的選擇 -- 分類與回歸 神經網絡可用于回歸問題和分類問題。 架構上的共同差異在于輸出層：為了能夠帶來實數為基礎的結果，不應應用諸如 Sigmoid 之類的標準化函數，這樣我們就不會將變量的結果更改為許多可能的類別值之一，獲得了可能的連續結果。 ## 有用的庫和方法 在本章中，我們將使用 TensorFlow 和工具庫中的一些新工具，這些是最重要的工具： ### TensorFlow 激活函數 TensorFlow 導航中最常用的函數： * `tf.sigmoid(x)`：標準 Sigmoid 函數 * `tf.tanh(x)`：雙曲正切 * `tf.nn.relu(features)`：Relu 傳遞函數 TensorFlow 導航的其他函數： * `tf.nn.elu(features)`：計算指數線性：如果`< 0`則為`exp(features) - 1`，否則為`features` * `tf.nn.softsign(features)`：計算 softsign：`features / (abs(features) + 1)` * `tf.nn.bias_add(value, bias)`：為值增加偏差 ### TensorFlow 損失優化方法 TensorFlow 損失優化方法如下所述： * `tf.train.GradientDescentOptimizer(learning_rate, use_locking, name)`：這是原始的梯度下降方法，僅具有學習率參數 * `tf.train.AdagradOptimizer(learning_rate, initial_accumulator_value, use_locking, name)`：此方法使學習率適應參數的頻率，從而提高了最小搜索稀疏參數的效率 * `tf.train.AdadeltaOptimizer(learning_rate, rho, epsilon, use_locking, name)`：這是改良的 AdaGrad，它將限制頻繁參數的累積到最大窗口，因此它考慮了一定數量的步驟，而不是整個參數歷史記錄。 * `tf.train.AdamOptimizer tf.train.AdamOptimizer.__init__(learning_rate, beta1, beta2, epsilon, use_locking, name)`：此方法在計算梯度時會添加一個因子，該因子對應于過去梯度的平均值，等同于動量因子。 因此，來自自適應矩估計的亞當這個名字。 ### Sklearn 預處理工具 讓我們看一下以下 Sklearn 預處理工具： * `preprocessing.StandardScaler()`：數據集的正則化是許多機器學習估計器的普遍要求，因此，為了使收斂更加直接，數據集將必須更像是標準正態分布，即具有零均值和單位方差的高斯曲線。 在實踐中，我們通常會忽略分布的形狀，而只是通過刪除每個特征的平均值來變換數據以使其居中，然后通過將非恒定特征除以它們的標準偏差來縮放它。 對于此任務，我們使用`StandardScaler`，它實現了前面提到的任務。 它還存儲轉換，以便能夠將其重新應用于測試集。 * `StandardScaler` 。 `fit_transform()`：簡單地將數據調整為所需格式。 `StandardScaler`對象將保存轉換變量，因此您將能夠取回非規格化數據。 * `cross_validation.train_test_split`：此方法將數據集分為訓練和測試段，我們只需要提供分配給每個階段的數據集的百分比即可。 # 第一個項目 -- 非線性一般函數回歸 人工神經網絡示例通常包含絕大多數分類問題，但實際上有大量應用可以表示為回歸。 用于回歸的網絡架構與用于分類問題的網絡架構沒有很大不同：它們可以采用多變量輸入，也可以使用線性和非線性激活函數。 在某些情況下，唯一必要的情況是僅在層的末尾刪除類似于 Sigmoid 的函數，以允許出現所有選項。 在第一個示例中，我們將對一個簡單的，有噪聲的二次函數進行建模，并將嘗試通過單個隱藏層網絡對其進行回歸，并查看我們可以多么接近地預測從測試總體中得出的值。 ## 數據集說明和加載 在這種情況下，我們將使用生成的數據集，該數據集與第 3 章的線性回歸中的數據集非常相似。 我們將使用常見的 Numpy 方法生成二次函數，然后添加隨機噪聲，這將有助于我們了解線性回歸如何推廣。 核心樣本創建例程如下： ```py import numpy as np trainsamples = 200 testsamples = 60 dsX = np.linspace(-1, 1, trainsamples + testsamples).transpose() dsY = 0.4* pow(dsX,2) +2 * dsX + np.random.randn(*dsX.shape) * 0.22 + 0.8 ``` ## 數據集預處理 該數據集在生成時不需要進行預處理，并且具有良好的屬性，例如居中并具有`-1, 1`的樣本分布。 ## 模型架構 -- 損失函數描述 此設置的損耗將簡單地用均方根誤差表示，如下所示： ```py cost = tf.pow(py_x-Y, 2)/(2) ``` ## 損失函數優化器 在這種情況下，我們將使用梯度下降成本優化器，可以通過以下代碼調用該優化器： ```py train_op = tf.train.AdamOptimizer(0.5).minimize(cost) ``` ## 準確率和收斂性測試 `predict_op = tf.argmax(py_x, 1)` ```py cost1 += sess.run(cost, feed_dict={X: [[x1]], Y: y1}) / testsamples ``` ### 示例代碼 讓我們看一下下面顯示的示例代碼： ```py import tensorflow as tf import numpy as np from sklearn.utils import shuffle %matplotlib inline import matplotlib.pyplot as plt trainsamples = 200 testsamples = 60 #Here we will represent the model, a simple imput, a hidden layer of sigmoid activation def model(X, hidden_weights1, hidden_bias1, ow): hidden_layer = tf.nn.sigmoid(tf.matmul(X, hidden_weights1)+ b) return tf.matmul(hidden_layer, ow) dsX = np.linspace(-1, 1, trainsamples + testsamples).transpose() dsY = 0.4* pow(dsX,2) +2 * dsX + np.random.randn(*dsX.shape) * 0.22 + 0.8 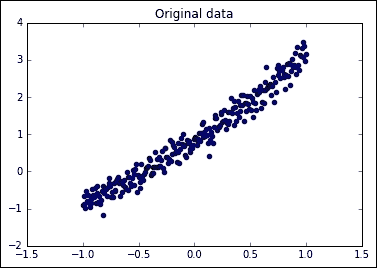plt.figure() # Create a new figure plt.title('Original data') plt.scatter(dsX,dsY) #Plot a scatter draw of the datapoints ```  ```py X = tf.placeholder("float") Y = tf.placeholder("float") # Create first hidden layer hw1 = tf.Variable(tf.random_normal([1, 10], stddev=0.1)) # Create output connection ow = tf.Variable(tf.random_normal([10, 1], stddev=0.0)) # Create bias b = tf.Variable(tf.random_normal([10], stddev=0.1)) model_y = model(X, hw1, b, ow) # Cost function cost = tf.pow(model_y-Y, 2)/(2) # construct an optimizer train_op = tf.train.GradientDescentOptimizer(0.05).minimize(cost) # Launch the graph in a session with tf.Session() as sess: tf.initialize_all_variables().run() #Initialize all variables for i in range(1,100): dsX, dsY = shuffle (dsX.transpose(), dsY) #We randomize the samples to mplement a better training trainX, trainY =dsX[0:trainsamples], dsY[0:trainsamples] for x1,y1 in zip (trainX, trainY): sess.run(train_op, feed_dict={X: [[x1]], Y: y1}) testX, testY = dsX[trainsamples:trainsamples + testsamples], dsY[0:trainsamples:trainsamples+testsamples] cost1=0. for x1,y1 in zip (testX, testY): cost1 += sess.run(cost, feed_dict={X: [[x1]], Y: y1}) / testsamples if (i%10 == 0): print "Average cost for epoch " + str (i) + ":" + str(cost1) ``` ## 結果描述 這是不同周期的結果的副本。請注意，由于這是一個非常簡單的函數，因此即使第一次迭代也具有非常好的結果： ```py Average cost for epoch 1:[[ 0.00753353]] Average cost for epoch 2:[[ 0.00381996]] Average cost for epoch 3:[[ 0.00134867]] Average cost for epoch 4:[[ 0.01020064]] Average cost for epoch 5:[[ 0.00240157]] Average cost for epoch 6:[[ 0.01248318]] Average cost for epoch 7:[[ 0.05143405]] Average cost for epoch 8:[[ 0.00621457]] Average cost for epoch 9:[[ 0.0007379]] ``` # 第二個項目 -- 非線性回歸和汽車的燃油效率建模 在此示例中，我們將進入一個區域，其中神經網絡可提供大部分附加價值； 解決非線性問題。 為了開始這一旅程，我們將基于幾個變量對幾種汽車模型的燃油效率建模一個回歸模型，該變量可以更好地用非線性函數表示。 ## 數據集說明和加載 對于這個問題，我們將分析一個非常著名的，標準的，格式正確的數據集，該數據集將使我們能夠分析一個多變量問題：根據離散和連續的一些相關變量來猜測汽車的 MPG。 這可以被認為是一個玩具，并且有些過時了，但是它將為更復雜的問題鋪平道路，并且具有已經被眾多書目分析的優勢。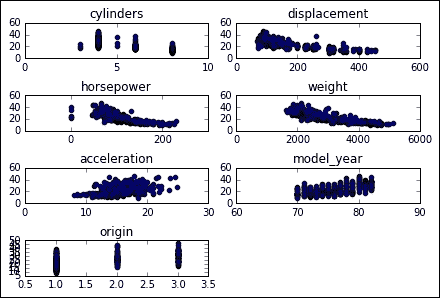 屬性信息 該數據集具有以下數據列： * `mpg`：連續 * `cylinders`：多值離散 * `displacement`：連續 * `horsepower`：連續 * `weight`：連續 * `acceleration`：連續 * `model year:`多值離散 * `origin`：多值離散 * `car name`：字符串（將不使用） 我們將不對數據進行詳細的分析，但是我們可以非正式地推斷出所有連續變量都與增加或減少目標變量相關：  ## 數據集預處理 對于此任務，我們將使用來自 sklearn 的上述縮放器對象： * `scaler = preprocessing.StandardScaler()` * `X_train = scaler.fit_transform(X_train)` ## 模型架構 我們將要構建的是一個前饋神經網絡，具有多變量輸入和簡單輸出：  ## 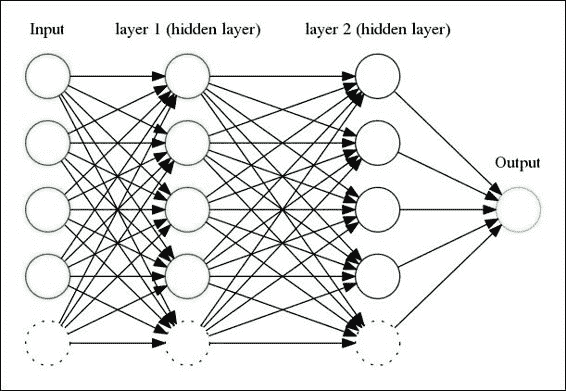收斂性測試 ```py score = metrics.mean_squared_error(regressor.predict(scaler.transform(X_test)), y_test) print('MSE: {0:f}'.format(score)) ``` ## 結果描述 ```py Step #99, avg. train loss: 182.33624 Step #199, avg. train loss: 25.09151 Step #300, epoch #1, avg. train loss: 11.92343 Step #400, epoch #1, avg. train loss: 11.20414 Step #500, epoch #1, avg. train loss: 5.14056 Total Mean Squared Error: 15.0792258911 ``` ```py %matplotlib inline import matplotlib.pyplot as plt import pandas as pd from sklearn import datasets, cross_validation, metrics from sklearn import preprocessing from tensorflow.contrib import skflow # Read the original dataset df = pd.read_csv("data/mpg.csv", header=0) # Convert the displacement column as float df['displacement']=df['displacement'].astype(float) # We get data columns from the dataset # First and last (mpg and car names) are ignored for X X = df[df.columns[1:8]] y = df['mpg'] plt.figure() # Create a new figure for i in range (1,8): number = 420 + i ax1.locator_params(nbins=3) ax1 = plt.subplot(number) plt.title(list(df)[i]) ax1.scatter(df[df.columns[i]],y) #Plot a scatter draw of the datapoints plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0) # Split the datasets X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.25) # Scale the data for convergency optimization scaler = preprocessing.StandardScaler() # Set the transform parameters X_train = scaler.fit_transform(X_train) # Build a 2 layer fully connected DNN with 10 and 5 units respectively regressor = skflow.TensorFlowDNNRegressor(hidden_units=[10, 5], steps=500, learning_rate=0.051, batch_size=1) # Fit the regressor regressor.fit(X_train, y_train) # Get some metrics based on the X and Y test data score = metrics.mean_squared_error(regressor.predict(scaler.transform(X_test)), y_test) print(" Total Mean Squared Error: " + str(score)) ``` # 第三個項目 -- 葡萄酒分類：多類分類的學習 在本節中，我們將使用更復雜的數據集，嘗試根據產地對葡萄酒進行分類。 ## 數據集說明和加載 該數據包含對來自意大利同一地區但來自三個不同品種的葡萄酒進行化學分析的結果。 分析確定了三種葡萄酒中每種所含 13 種成分的數量。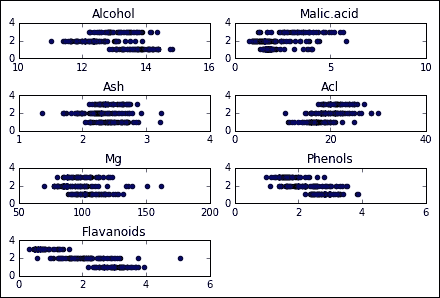 數據變量： * 醇 * 蘋果酸 * 灰 * 灰的堿度 * 鎂 * 總酚 * 黃酮 * 非類黃酮酚 * 花青素 * 色彩強度 * 色調 * 稀釋酒的 OD280/OD315 * 脯氨酸 要讀取數據集，我們將僅使用提供的 CSV 文件和熊貓： ```py df = pd.read_csv("./wine.csv", header=0) ```  ## 數據集預處理 隨著 csv 上的值從 1 開始，我們將歸一化帶有偏差的值： ```py y = df['Wine'].values-1 ``` 對于結果，我們將這些選項表示為一個數組的熱門列表： ```py Y = tf.one_hot(indices = y, depth=3, on_value = 1., off_value = 0., axis = 1 , name = "a").eval() ``` 我們還將預先洗凈值： ```py X, Y = shuffle (X, Y) scaler = preprocessing.StandardScaler() X = scaler.fit_transform(X) ``` ## 模型架構 這個特定的模型將由一個單層，全連接的神經網絡組成： * `x` = `tf.placeholder(tf.float32, [None, 12])` * `W` = `tf.Variable(tf.zeros([12, 3]))` * `b` = `tf.Variable(tf.zeros([3]))` * `y` = `tf.nn.softmax(tf.matmul(x, W) + b)` ## 損失函數說明 我們將使用交叉熵函數來衡量損失： ```py y_ = tf.placeholder(tf.float32, [None, 3]) cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1])) ``` ## 損失函數優化器 同樣，將使用“梯度下降”方法來減少損失函數： ```py train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy) ``` ## 收斂測試 在收斂性測試中，我們將每個良好的回歸均轉換為 1，將每個錯誤的回歸均轉換為 0，然后獲取值的平均值來衡量模型的準確率： ```py correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(accuracy.eval({x: Xt, y_: Yt})) ``` ## 結果描述 如我們所見，隨著歷時的發展，我們具有可變精度，但是它總是優于 90% 的精度，具有 30% 的隨機基數（如果我們生成 0 到 3 之間的隨機數來猜測結果）。 ```py 0.973684 0.921053 0.921053 0.947368 0.921053 ``` ## 完整源代碼 讓我們看一下完整的源代碼： ```py sess = tf.InteractiveSession() import pandas as pd # Import data from tensorflow.examples.tlutorials.mnist import input_data from sklearn.utils import shuffle import tensorflow as tf from sklearn import preprocessing flags = tf.app.flags FLAGS = flags.FLAGS df = pd.read_csv("./wine.csv", header=0) print (df.describe()) #df['displacement']=df['displacement'].astype(float) X = df[df.columns[1:13]].values y = df['Wine'].values-1 Y = tf.one_hot(indices = y, depth=3, on_value = 1., off_value = 0., axis = 1 , name = "a").eval() X, Y = shuffle (X, Y) scaler = preprocessing.StandardScaler() X = scaler.fit_transform(X) # Create the model x = tf.placeholder(tf.float32, [None, 12]) W = tf.Variable(tf.zeros([12, 3])) b = tf.Variable(tf.zeros([3])) y = tf.nn.softmax(tf.matmul(x, W) + b) # Define loss and optimizer y_ = tf.placeholder(tf.float32, [None, 3]) cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1])) train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy) # Train tf.initialize_all_variables().run() for i in range(100): X,Y =shuffle (X, Y, random_state=1) Xtr=X[0:140,:] Ytr=Y[0:140,:] Xt=X[140:178,:] Yt=Y[140:178,:] Xtr, Ytr = shuffle (Xtr, Ytr, random_state=0) #batch_xs, batch_ys = mnist.train.next_batch(100) batch_xs, batch_ys = Xtr , Ytr train_step.run({x: batch_xs, y_: batch_ys}) cost = sess.run (cross_entropy, feed_dict={x: batch_xs, y_: batch_ys}) # Test trained model correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(accuracy.eval({x: Xt, y_: Yt})) ``` # 總結 在本章中，我們已經開始著手實現 TensorFlow 能力的真正替代物：神經網絡模型。 我們還看到了在回歸和分類任務中使用簡單神經網絡，簡單生成模型和實驗模型的情況。 在下一章中，我們將以卷積神經網絡的形式提高新架構的知識以及將神經網絡范式應用于其他知識領域（例如計算機視覺）的方式。