# 二、深度神經網絡 在上一章中，我們研究了簡單的 TensorFlow 操作以及如何在字體分類問題上使用邏輯回歸。 在本章中，我們將深入探討一種最流行和成功的機器學習方法-神經網絡。 使用 TensorFlow，我們將構建簡單和深度的神經網絡，以改善字體分類問題的模型。 在這里，我們將實踐神經網絡的基礎。 我們還將使用 TensorFlow 構建和訓練我們的第一個神經網絡。 然后，我們將進入具有神經元隱藏層的神經網絡，并完全理解它。 完成后，您將更好地掌握以下主題： * 基本神經網絡 * 單隱藏層模型 * 單隱藏層說明 * 多隱藏層模型 * 多隱藏層的結果 在第一部分中，我們將回顧神經網絡的基礎。 您將學習轉換輸入數據的常見方法，了解神經網絡如何將這些轉換聯系在一起，最后，如何在 TensorFlow 中實現單個神經元。 # 基本神經網絡 我們的邏輯回歸模型運作良好，但本質上是線性的。 將像素的強度加倍會使像素對得分的貢獻增加一倍，但我們可能只真正關心像素是否在某個閾值之上或將較小的權重放在較小的值上。 線性可能無法捕獲問題的所有細微差別。 解決此問題的一種方法是使用非線性函數轉換輸入。 讓我們看一下 TensorFlow 中的一個簡單示例。 首先，請確保加載所需的模塊（`tensorflow`，`numpy`和`math`）并啟動交互式會話： ```py import tensorflow as tf import numpy as np import math sess = tf.InteractiveSession() ``` 在下面的示例中，我們創建了三個五長向量的正常隨機數，這些向量被截斷以防止它們過于極端，中心不同： ```py x1 = tf.Variable(tf.truncated_normal([5], mean=3, stddev=1./math.sqrt(5))) x2 = tf.Variable(tf.truncated_normal([5], mean=-1, stddev=1./math.sqrt(5))) x3 = tf.Variable(tf.truncated_normal([5], mean=0, stddev=1./math.sqrt(5))) sess.run(tf.global_variables_initializer()) ``` ### 注意 請注意，由于這是隨機的，因此您的值可能會有所不同，但這很好。 常見的轉換是對輸入求平方。 這樣做會使更大的值變得更加極端，當然也使所有事情都變得積極起來： ```py sqx2 = x2 * x2 print(x2.eval()) print(sqx2.eval()) ``` 您可以在以下屏幕截圖中看到結果：  ## 對數函數 相反，如果您需要在較小的值中有更多細微差別，則可以嘗試采用輸入的自然對數或任何基本對數： ```py logx1 = tf.log(x1) print(x1.eval()) print(logx1.eval()) ``` 請參考以下屏幕截圖，請注意，較大的值往往會擠在一起，而較小的值則散布得多：  但是，對數不能處理負輸入，并且您越接近零，小輸入就變得越負。 因此，請注意對數。 最后，是 Sigmoid 變換。 ## sigmoid 函數 不必擔心公式，只需知道正負兩個極值分別被壓縮為加一或零，而接近零的輸入就接近二分之一： ```py sigx3 = tf.sigmoid(x3) print(x3.eval()) print(sigx3.eval()) ``` 在這里，您將看到一個接近一半的示例。 它從四分之一開始，到現在將近一半：  在機器學習中，我們通常將這些轉換稱為激活函數。 我們通常將輸入的加權總和組合到其中。 當您考慮輸入，權重和激活函數時，就將其稱為神經元，因為它是受生物神經元啟發的。 真正的神經元如何在物理大腦中工作的細節不在本書的討論范圍之內。 如果您對此感興趣，則神經生物學文章可能包含更多內容，或者您??可以參考 Gordon M. Shepherd 的《神經元學說》作為近期參考。 讓我們看一下 TensorFlow 中的一個簡單示例： ```py w1 = tf.constant(0.1) w2 = tf.constant(0.2) sess.run(tf.global_variables_initializer()) ``` 首先，只需創建一些常量`w1`和`w2`即可。 我們將`x1`乘以`w1`，將`x2`乘以`w2`，然后將這些中間值相加，最后將結果通過`tf.sigmoid`的`sigmoid`激活函數進行處理。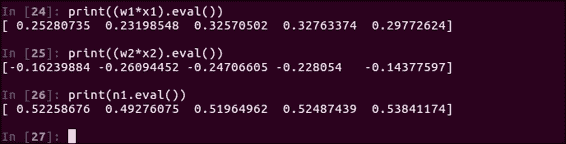 查看以下屏幕快照中顯示的結果：  同樣，現在不必擔心確切的公式，您可以擁有各種不同的激活函數。 請注意，這是您邁向自己的神經網絡的第一步。 那么，我們如何從單個神經元到整個網絡？ 簡單！ 一個神經元的輸入僅成為網絡下一層中另一神經元的輸入。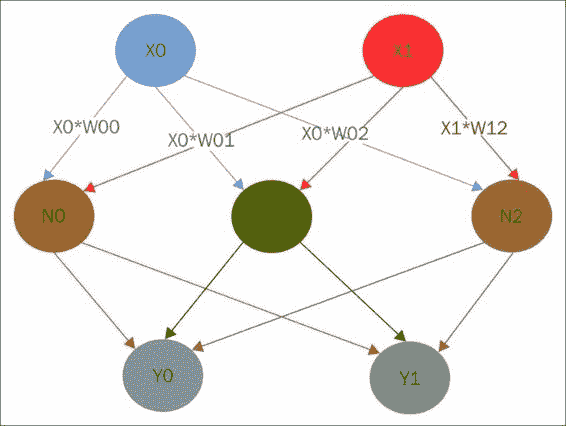  在上圖中，我們有一個簡單的網絡，其中有兩個輸入`X0`和`X1`，兩個輸出`Y0`和`Y1`，中間有三個神經元。 `X0`中的值被發送到每個`N`神經元，但是權重不同，該權重乘以與每個相關的`X0`。 `X1`也發送到每個神經元，并具有自己的一組權重。 對于每個神經元，我們計算輸入的加權總和，將其通過激活函數，然后產生中間輸出。 現在，我們做同樣的事情，但是將神經元的輸出視為`Y`的輸入。 注意，通過對輸入加權和進行非線性激活，我們實際上只是為最終模型計算了一組新的特征。 現在您已經了解了 TensorFlow 中非線性轉換的基礎以及什么是神經網絡。 好吧，它們可能不會讓您讀懂思想，它們對于深度學習至關重要。 在下一節中，我們將使用簡單的神經網絡來改進分類算法。 # 單隱藏層模型 在這里，我們將實踐神經網絡的基礎知識。 我們將邏輯回歸 TenserFlow 代碼改編為神經元的單個隱藏層。 然后，您將學習反向傳播背后的思想以計算權重，即訓練網絡。 最后，您將在 TensorFlow 中訓練您的第一個真正的神經網絡。 本部分的 TensorFlow 代碼應該看起來很熟悉。 它只是邏輯回歸代碼的略微演變版本。 讓我們看看如何添加神經元的隱藏層，以計算輸入像素的非線性組合。 您應該從全新的 Python 會話開始，執行代碼以讀入，并按照邏輯模型中的步驟設置數據。 相同的代碼，只是復制到新文件中： ```py import tensorflow as tf import numpy as np import math from tqdm import tqdm %autoindent try: from tqdm import tqdm except ImportError: def tqdm(x, *args, **kwargs): return x ``` 您總是可以回到前面的部分，并提醒自己該代碼的作用； 直到`num_hidden`變量的所有內容都可以使您快速入門。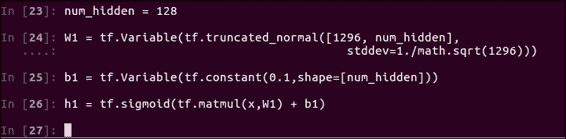 ## 探索單隱藏層模型 現在，讓我們逐步介紹單個隱藏層模型： 1. 首先，讓我們指定`num_hidden = 128`想要多少個神經元； 最終，這實際上是將多少個非線性組合傳遞給邏輯對數。 2. 為了適應這一點，我們還需要更新`W1`和`b1`權重張量的形狀。 他們現在正在饋送我們隱藏的神經元，因此需要匹配形狀： ```py W1 = tf.Variable(tf.truncated_normal([1296, num_hidden], stddev=1./math.sqrt(1296))) b1 = tf.Variable(tf.constant(0.1,shape=[num_hidden])) ``` 3. 我們計算加權和的激活函數的方法是使用單行`h1`。 這是將我們的輸入像素乘以每個神經元各自的權重： ```py h1 = tf.sigmoid(tf.matmul(x,W1) + b1) ``` 添加神經元偏差項，最后通過`sigmoid`激活函數進行設置； 此時，我們有 128 個中間值：  4. 現在，這只是對您友好的邏輯回歸； 您已經知道該怎么辦。 這些新計算的 128 個特征需要它們自己的權重和偏置集來計算輸出類的分數，分別為`W2`和`b2`。 注意形狀如何與神經元的形狀 128 匹配，并且輸出類的數量為 5： ```py W2 = tf.Variable(tf.truncated_normal([num_hidden, 5], stddev=1./math.sqrt(5))) b2 = tf.Variable(tf.constant(0.1,shape=[5])) sess.run(tf.global_variables_initializer()) ``` 在所有這些權重中，我們使用此奇怪的截斷普通調用對其進行初始化。 借助神經網絡，我們希望獲得良好的初始值分布，以便我們的權重可以攀升至有意義的值，而不是僅僅歸零。 5. 截斷正態具有給定標準偏差的正態分布中的隨機值，該研究標準按輸入數量進行縮放，但拋出的值太極端，因此被截斷了。 定義好權重和神經元后，我們將像以前一樣設置最終的`softmax`模型，除了需要注意使用 128 個神經元作為輸入`h1`以及相關的權重和偏差`W2`和`b2`： ```py y = tf.nn.softmax(tf.matmul(h1,W2) + b2) ``` ## 反向傳播 訓練神經網絡和許多其他機器學習模型權重的關鍵稱為反向傳播。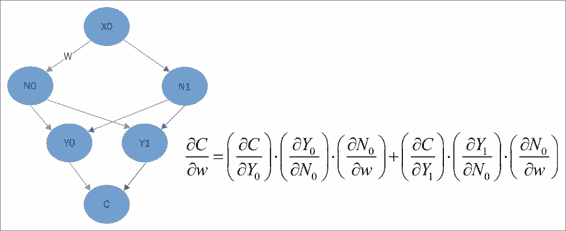  完整的推導超出了本書的范圍，但是讓我們直觀地進行研究。 當您在空中訓練邏輯回歸之類的模型并且訓練集直接來自選擇不當的權重時，您可以看到應該調整哪些權重以及應該調整多少權重并相應地更改它們。 從形式上講，TensorFlow 通過計算空氣相對于權重的導數并將權重調整為該數值的一小部分來實現此目的。 反向傳播實際上是同一過程的擴展。 您從最底層的輸出或成本函數層開始，計算導數，然后使用它們來計算與上一層神經元相關的導數。 通過將從成本到權重的路徑上的導數乘積相加，我們可以計算相對于要調整的權重的成本的適當偏導數。 上圖中顯示的公式僅說明了紅色箭頭顯示的內容。 如果這看起來很復雜，請不要擔心。 TensorFlow 使用優化器在后臺為您處理。 由于我們使用 TensorFlow 精心指定了模型來訓練模型，因此幾乎與之前完全相同，因此我們將在此處使用相同的代碼： ```py epochs = 5000 train_acc = np.zeros(epochs//10) test_acc = np.zeros(epochs//10) for i in tqdm(range(epochs), ascii=True): if i % 10 == 0: # Record summary data, and the accuracy # Check accuracy on train set A = accuracy.eval(feed_dict={x: train.reshape([-1,1296]), y_: onehot_train}) train_acc[i//10] = A # And now the validation set A = accuracy.eval(feed_dict={x: test.reshape([-1,1296]), y_: onehot_test}) test_acc[i//10] = A train_step.run(feed_dict={x: train.reshape([-1,1296]), y_: onehot_train}) ``` 需要注意的一件事是，因為我們有這些隱藏的神經元，所以有更多的權重可以擬合模型。 這意味著我們的模型將需要更長的運行時間，并且必須花費更多的迭代時間才能進行訓練。 這次我們通過`5000`歷時運行它：  該模型可能比以前的模型花費更長的時間，可能是前一個模型的四倍。 因此，您可能需要幾分鐘到 10 分鐘的時間，具體取決于您的計算機。 現在，通過模型訓練，我們將在稍后查看驗證準確率。 # 單隱藏層的說明 在本節中，我們將仔細研究構建的模型。 首先，我們將驗證模型的整體準確率，然后查看模型出了哪些問題。 最后，我們將可視化與多個神經元相關的權重，以查看它們在尋找什么： ```py plt.figure(figsize=(6, 6)) plt.plot(train_acc,'bo') plt.plot(test_acc,'rx') ``` 確保您已經按照上一節中的步驟訓練了模型，如果沒有，您可能要在這里停下來并首先進行操作。 由于我們每隔 10 個訓練周期就評估模型的準確率并保存結果，因此現在很容易探索模型的演變方式。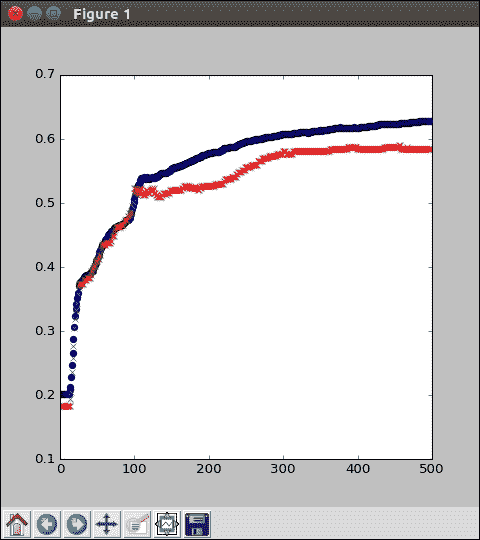 使用 Matplotlib，我們可以在同一張圖上繪制訓練精度（藍色點）和測試精度（紅色點）：  同樣，如果您沒有 Matplotlib，那就沒關系。 您可以只查看數組值本身。 請注意，訓練精度（藍色）通常比測試精度（紅色）好一點。 這并不奇怪，因為測試圖像對于模型來說是全新的，并且可能包含以前看不見的特征。 另外，觀察精度通常會攀升到更多的周期，然后逐漸上升，然后逐漸上升。 我們的模型在這里達到約 60% 的準確率； 并非完美，但對簡單邏輯回歸進行了改進。 要查看我們的模型在哪里混淆，創建混淆矩陣會很有幫助。 也就是說，我們將尋找一個可以說的實際繪圖類別。 該模型將其分類為什么？ 形式上是`5x5`矩陣。 對于每個測試圖像，如果圖像實際上是類別`i`和模型預測類別`j`，則我們增加值和位置`i j`。 請注意，當模型正確時，則為`i = j`。 一個好的模型在對角線上將具有很大的值，而在其他地方則沒有很多。 通過這種類型的分析，很容易看出兩個類是否經常彼此混淆，或者模型很少選擇某些類。 在以下示例中，我們通過求值`y`（類概率）來創建預測類： ```py pred = np.argmax(y.eval(feed_dict={x: test.reshape([-1,1296]), y_: onehot_test}), axis = 1) conf = np.zeros([5,5]) for p,t in zip(pred,np.argmax(onehot_test,axis=1)): conf[t,p] += 1 plt.matshow(conf) plt.colorbar() ``` `np.argmax`函數提取概率最大的位置。 同樣，為了確定實際的類別，我們使用`np.argmax`撤消一次熱編碼。 創建混亂矩陣始于全零數組，然后逐步遍歷所有填充的測試數據。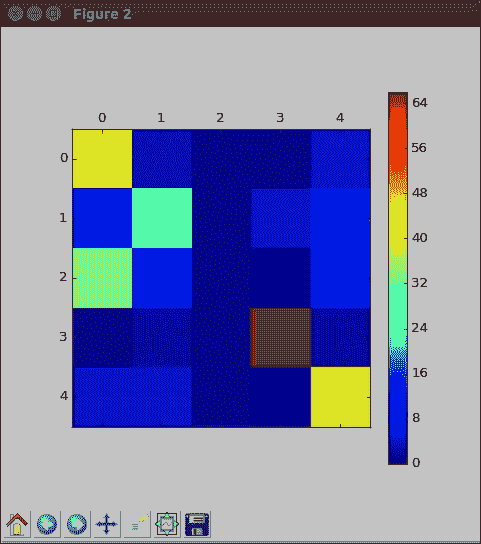Matplotlib 讓我們看一下彩色圖像，但打印與會者的效果幾乎相同：  在前面的輸出中，我們看到模型通常做得不錯，只是它很少預測類`2`。 由于初始的隨機性，您的確切結果可能看起來有些不同。 ## 了解模型的權重 正如我們查看邏輯回歸模型的權重一樣，我們可以監視此模型的權重： ```py plt.figure(figsize=(6, 6)) f, plts = plt.subplots(4,8, sharex=True) for i in range(32): plts[i//8, i%8].pcolormesh(W1.eval()[:,i].reshape([36,36])) ``` 但是，現在我們有 128 個神經元，每個神經元的權重都來自輸入像素，權重為`36x36`。 讓我們看看其中的一些，以了解他們的發現。 同樣，如果您沒有 Matplotlib，則可以簡單地打印出數組以查看相同的行為。 在這里，我們將研究 128 個神經元中的 32 個。 因此，讓我們將子圖的格式設置為四行八列。 現在，我們逐步求值每個神經元的權重，并將其重塑為圖像大小。 雙斜杠（`//`）使用整數除法將圖像放入適當的行，而百分號（`%`）使用余數（實際上是模塊化算術）來選擇列。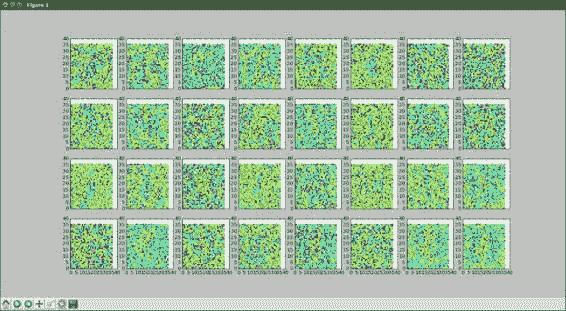  視覺上，在前面的輸出中，您可以看到一些形狀突出。 與它們的權重模式相比，某些神經元或多或少具有圓形形狀。 其他人看起來很隨意，但可能會選擇我們不容易理解的特征。 我們也可以嘗試可視化輸出層的權重，但是這些不再直觀。 我們稱其為神經網絡。 現在，輸出邏輯回歸是 128 個輸入值，以及用于計算 5 個分數的權重。 不再有圖像結構，因為每個像素都進入了隱藏層的每個神經元。 現在您知道了如何評估和解釋神經網絡結果。 做得好！ # 多隱藏層模型 在本節中，我們將向您展示如何使用其他隱藏層構建更復雜的模型。 我們將單層隱藏模型改編為稱為深度神經網絡的多層模型。 然后，我們將討論選擇要使用的神經元和層數。 最后，我們將耐心地訓練模型本身，因為這可能需要一段時間才能計算出來。 還記得我們向邏輯回歸模型添加神經元的隱藏層嗎？ 好了，我們可以再做一次，在我們的單個隱藏層模型中添加另一層。 一旦您擁有一層以上的神經元，我們就將其稱為深度神經網絡。 但是，您以前所學的一切都可以立即應用。 與本章前面的部分一樣，您應該進行一個全新的 Python 會話并執行本部分代碼文件中直到`num_hidden1`的代碼。 然后，樂趣開始了。  ## 探索多隱藏層模型 首先，將舊的`num_hidden`更改為`num_hidden1`，以指示第一個隱藏層上的神經元數量： ```py # Hidden layer 1 num_hidden1 = 128 ``` 確保更改變量，同時定義權重和偏差變量。 現在，我們將插入第二個隱藏層： ```py W1 = tf.Variable(tf.truncated_normal([1296,num_hidden1], stddev=1./math.sqrt(1296))) b1 = tf.Variable(tf.constant(0.1,shape=[num_hidden1])) h1 = tf.sigmoid(tf.matmul(x,W1) + b1) ``` 這次使用帶有`32`神經元的神經元。 請注意，權重的形狀必須如何解釋來自上一層的 128 個中間輸出中的每一個進入當前層的 32 個輸入或神經元，但是我們初始化權重和偏差的方式基本上相同： ```py # Hidden Layer 2 num_hidden2 = 32 W2 = tf.Variable(tf.truncated_normal([num_hidden1, num_hidden2],stddev=2./math.sqrt(num_hidden1))) b2 = tf.Variable(tf.constant(0.2,shape=[num_hidden2])) h2 = tf.sigmoid(tf.matmul(h1,W2) + b2) ``` 如您在前面的代碼中所見，我們像以前一樣使用`sigmoid`函數創建`h2`輸出，并使用矩陣乘法，加法和函數調用。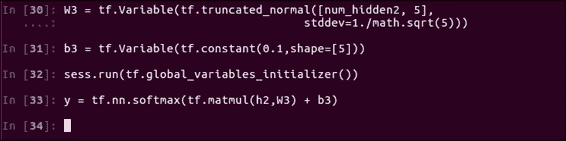 對于輸出邏輯回歸層，我們只需要更新變量名稱： ```py # Output Layer W3 = tf.Variable(tf.truncated_normal([num_hidden2, 5], stddev=1./math.sqrt(5))) b3 = tf.Variable(tf.constant(0.1,shape=[5])) ``` 現在這是第三組權重，當然，此形狀必須與前面的隱藏層的輸出匹配，因此`32 x 5`：  不要忘記使用`h2`，`W3`和`b3`變量更新`y`模型函數。 您不想只使用舊模型就更新所有代碼。 您可能想知道我們如何決定第一層的 128 個神經元和第二層的 32 個神經元。 事實是，為網絡確定合適的尺寸和形狀可能是一個具有挑戰性的問題。 盡管計算可能會很昂貴，但是反復試驗是開發模型的一種方法。 通常，您可能會從舊模型開始并從那里開始工作。 在這里，我們從 128 個神經元的單個隱藏層開始，然后嘗試在其下添加一個新層。 我們要計算一些特征以區分五類，因此在選擇神經元數量時應牢記這一點。 通常，最好從小處著手，逐步發展到解釋數據的最小模型。 如果在頂層具有 128 個神經元而在下一層具有 8 個神經元的模型的效果較差，則可能表明我們需要為最后一層提供更多特征，并應添加更多而不是更少的神經元。 嘗試將最后一層中的神經元數量加倍，當然，最好回到較早的層并調整那里的神經元數量。 同樣，您可以更改優化器的學習率，從而改變每一步調整權重的程度，甚至更改用于優化的函數。 ### 注意 設置所有這些值稱為超參數優化，這是機器學習研究中的熱門話題。 請注意，我們實際上是從最簡單的模型，邏輯回歸開始，然后慢慢添加新的功能和結構。 如果一個簡單的模型運行良好，那么甚至沒有必要花時間在更高級的東西上。 現在已經指定了我們的模型，讓我們實際進行訓練： ```py # Climb on cross-entropy cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(logits= y + 1e-50, labels= y_)) # How we train train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy) # Define accuracy correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1)) accuracy=tf.reduce_mean(tf.cast(correct_prediction, "float")) ``` 同樣，我們需要在 T??ensorFlow 圖中重新定義我們的訓練節點，但是這些與以前完全相同。 請注意，由于我們的第一個隱藏層現在掛接到神經元的另一層，因此我們需要計算更多的權重。 以下是實際的訓練代碼： ```py epochs = 25000 train_acc = np.zeros(epochs//10) test_acc = np.zeros(epochs//10) for i in tqdm(range(epochs)): # Record summary data, and the accuracy if i % 10 == 0: # Check accuracy on train set A = accuracy.eval(feed_dict={ x: train.reshape([-1,1296]), y_: onehot_train}) train_acc[i//10] = A # And now the validation set A = accuracy.eval(feed_dict={ x: test.reshape([-1,1296]), y_: onehot_test}) test_acc[i//10] = A train_step.run(feed_dict={ x: train.reshape([-1,1296]), y_: onehot_train}) ``` 以前，我們有 128 乘以 5 的權重，但是現在我們有 128 乘以 32 的權重-這是該層的六倍，這是從像素到神經元第一層的初始權重之上。 深度神經網絡的一個缺點是它們可能需要一段時間才能訓練。 在這里，我們將運行`25000`個周期，以確保權重收斂：  這可能需要一個小時或更長時間，具體取決于您的計算機和 GPU。 盡管這看起來似乎過多，但專業的機器學習研究人員通常會訓練模型長達兩個星期。 您可能會學得很快，但是計算機需要一些時間。 在本節中，我們使用 TensorFlow 構建并訓練了一個真正的深度神經網絡。 許多專業的機器學習模型沒有您已經編寫的復雜。 # 多隱藏層的結果 現在，我們將研究深度神經網絡內部的情況。 首先，我們將驗證模型的準確率。 然后，我們將可視化并研究像素權重。 最后，我們還將查看輸出權重。 訓練完您的深度神經網絡后，讓我們看一下模型的準確率。 我們將以與單隱藏層模型相同的方式進行操作。 這次的唯一區別是，從更多的周期開始，我們保存了更多的訓練和測試準確率樣本。 和往常一樣，如果您沒有 Matplotlib，請不要擔心。 打印數組的一部分很好。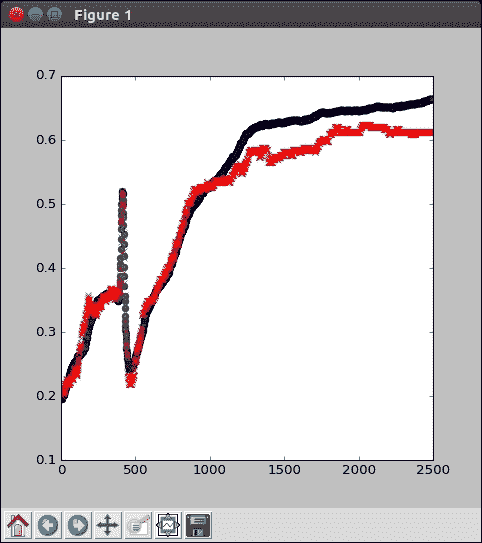 ## 了解多隱藏層的圖 執行以下代碼以查看結果： ```py # Plot the accuracy curves plt.figure(figsize=(6,6)) plt.plot(train_acc,'bo') plt.plot(test_acc,'rx') ```  從前面的輸出圖中，我們可以達到約 68% 的訓練精度，也許還有 63% 的驗證精度。 這還不錯，但是確實留出了一些改進的空間。 讓我們花點時間看一下準確率在許多周期如何增長。 當然，它起步非常糟糕，并且存在一些最初的麻煩，但是權重是隨機的，并且在那個時候仍在學習，并且在最初的數千個周期中它很快得到了改善。 雖然可能會暫時卡在局部最大值中，但通常會爬出并最終減慢其重音。 請注意，它仍然可以很好地進入訓練階段。 只是到了盡頭，模型才可能達到其最大容量。 根據隨機初始化，您的曲線可能看起來有些不同，但這沒關系； 這是您的模型，非常好。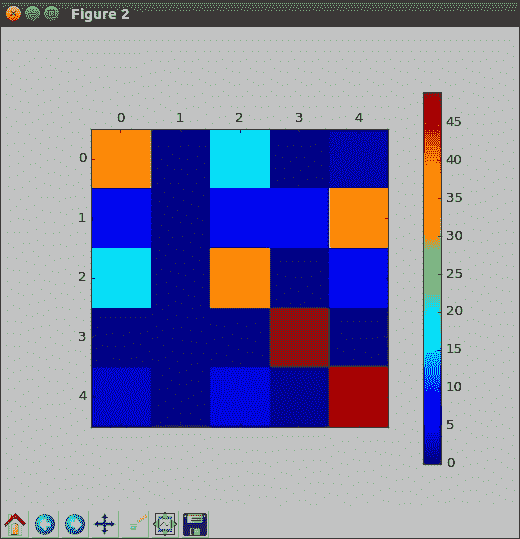 要查看我們的模型在哪里出現問題，讓我們看一下混淆矩陣： ```py pred = np.argmax(y.eval(feed_dict={x: test.reshape([-1,1296]), y_: onehot_test}), axis = 1) conf = np.zeros([5,5]) for p,t in zip(pred,np.argmax(onehot_test,axis=1)): conf[t,p] += 1 plt.matshow(conf) plt.colorbar() ``` 同樣，這與我們用于單個隱藏層模型的過程完全相同，只是在更高級的方面：  對此進行繪圖，就像在前面的輸出中一樣，我們看到該模型總體上運行良好，但是仍然難以識別其中一個類，這次是`1`。 我們正在逐步取得進展。 驗證準確率之后，讓我們檢查一下我們的第一層神經元，即 128 個人，發現了什么樣的現象： ```py # Let's look at a subplot of some weights f, plts = plt.subplots(4,8, sharex=True) for i in range(32): plts[i//8, i%8].matshow(W1.eval()[:,i].reshape([36,36])) ``` 為了簡單起見，我們僅查看前 32 個此類神經元。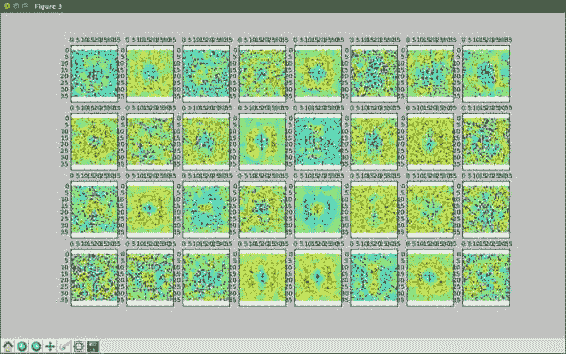 使用與先前模型相同的代碼，可以輕松地使用 Matplotlib 進行繪制或打印出來：  毫不奇怪，我們看到了許多與先前模型相同的函數。 盡管在這里，由于隨機初始化，即使它們看起來像是同一類型的特征，它們也會位于不同的位置。 同樣，您有一些環形神經元，具有非常條紋狀特征的神經元，以及具有寬條紋狀特征的另一個神經元。 就我們的神經網絡而言，圓形和條紋形狀是確定字體類別的良好成分。 盡管我們其他隱藏層中的權重不再具有圖像的結構，但查看輸出的權重可能會很有幫助。 這將告訴我們每個最終神經元對每個類別的貢獻。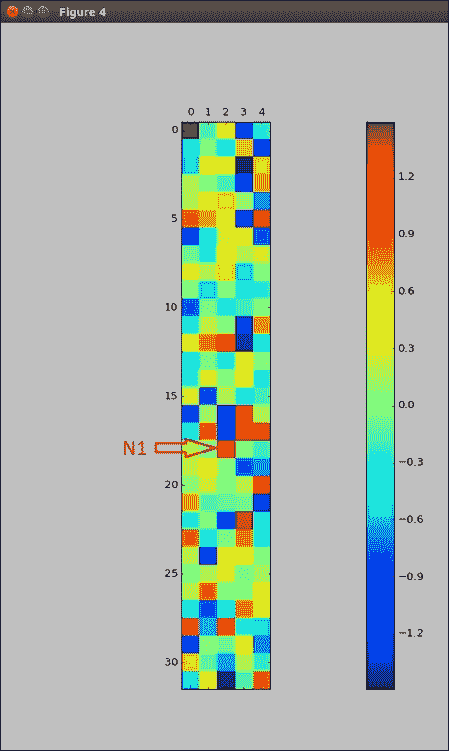 我們可以將其繪制為熱力圖，或使用`W3.eval`任意方式打印單個數組： ```py # Examine the output weights plt.matshow(W3.eval()) plt.colorbar() ``` 因為我們仔細指定了`W3`，所以每一行將代表一個神經元，每一列將代表一個類：  從前面的輸出圖中我們可以看到，不同的神經元對某些類別的貢獻要大于其他類別，這表明神經元正在計算的某些總體非線性特征與該特定字體類別有關。 也就是說，雖然這些神經元產生的值用于計算每種字體的分數，但非常重要且權重較大的一種字體的神經元可能與另一種字體幾乎無關。 例如，對于`2`類，`N1`神經元的權重非常大，而對于所有其他類別，`N1`神經元的權重幾乎為零。 該神經元具有什么計算特征，對于`2`類而言非常重要，但對于其他類別而言則沒有那么重要。 # 總結 在本章中，我們使用 TensorFlow 進行了深度學習。 盡管我們從一個神經元隱藏層的簡單模型開始，但是并不需要花很長時間就可以開發和訓練用于字體分類問題的深度神經網絡。 您了解了單層和多層隱藏層模型，并對其進行了詳細了解。 您還將了解神經網絡的不同類型，并使用 TensorFlow 構建和訓練了我們的第一個神經網絡。 在下一章中，我們將使用卷積神經網絡（一種用于圖像分類的強大工具）來證明我們的模型。