# 十一、生成模型和 CapsNet 在本章中，我們將介紹一些用于以下方面的方法： * 學習使用簡單 GAN 偽造 MNIST 圖像 * 學習使用 DCGAN 偽造 MNIST 圖像 * 學習使用 DCGAN 偽造名人面孔和其他數據集 * 實現變分自編碼器 * 通過膠囊網絡學習擊敗 MNIST 的最新結果 # 介紹 在本章中，我們將討論如何將**生成對抗網絡**（**GAN**）用于深度學習領域，其中關鍵方法是訓練圖像生成器來挑戰鑒別器，并同時訓練鑒別器來改進生成器。 可以將相同的方法應用于不同于圖像領域。 另外，我們將討論變分自編碼器。 GAN 已被深度學習之父之一 Yann LeCun 定義為[“這是深度學習的突破”](https://www.quora.com/What-are-some-recent-and-potentially-upcoming-breakthroughs-in-deep-learning)。 GAN 能夠學習如何再現看起來真實的合成數據。 例如，計算機可以學習如何繪制和創建逼真的圖像。 這個想法最初是由與蒙特利爾大學 Google Brain 合作的 Ian Goodfellow 提出的，最近由 [OpenAI](https://openai.com/) 提出。 # 那么，GAN 是什么？ 通過將其視為類似于*藝術偽造*的方式，可以很容易地理解 GAN 的關鍵過程，這是創作被誤認為其他人（通常是更著名的藝術家）的藝術品的過程。 GAN 同時訓練兩個神經網絡。 **生成器**`G(Z)`是生成贗品，而**鑒別器**`D(Y)`可以根據對真實藝術品和復制品的觀察來判斷復制品的逼真度。 `D(Y)`接受輸入 Y（例如圖像），并投票決定輸入的真實程度。 通常，接近零的值表示*真實*，而接近一的值表示*偽造*。`G(Z)`從隨機噪聲`Z`中獲取輸入，并訓練自己以欺騙 D 認為`G(Z)`產生的任何東西都是真實的。 因此，訓練鑒別器`D(Y)`的目標是，從為每個來自真實數據分布的圖像最大化`D(Y)`，并為每個不來自真實數組的圖像最小化`D(Y)`，而不是來自真實數據分布的每個圖像。 因此，G 和 D 扮演相反的游戲：因此稱為對抗訓練。 請注意，我們以交替的方式訓練 G 和 D，其中它們的每個目標都表示為通過梯度下降優化的損失函數。 生成模型學習如何越來越好地進行偽造，而鑒別模型學習如何越來越好地識別偽造。 鑒別器網絡（通常是標準卷積神經網絡）試圖對輸入圖像是真實的還是生成的進行分類。 一個重要的新思想是反向傳播鑒別器和生成器，以調整生成器的參數，以使生成器可以學習如何在越來越多的情況下欺騙鑒別器。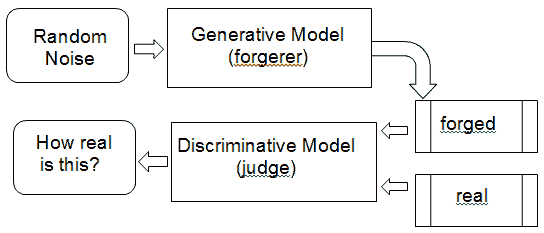 最后，生成器將學習如何生成與真實圖像無法區分的圖像：  生成器（偽造）- 鑒別器（判斷）模型的示例。 鑒別器接收偽造的真實圖像 當然，GAN 可以在有兩名玩家的游戲中找到平衡點。 為了有效學習，如果一個玩家在下一輪更新中成功下坡，那么相同的更新也必須使另一個玩家也下坡。 想想看！ 如果偽造者每次都學會如何愚弄法官，那么偽造者本人就沒什么可學的了。 有時，兩個玩家最終會達到平衡，但這并不總是可以保證的，因此兩個玩家可以長時間繼續比賽。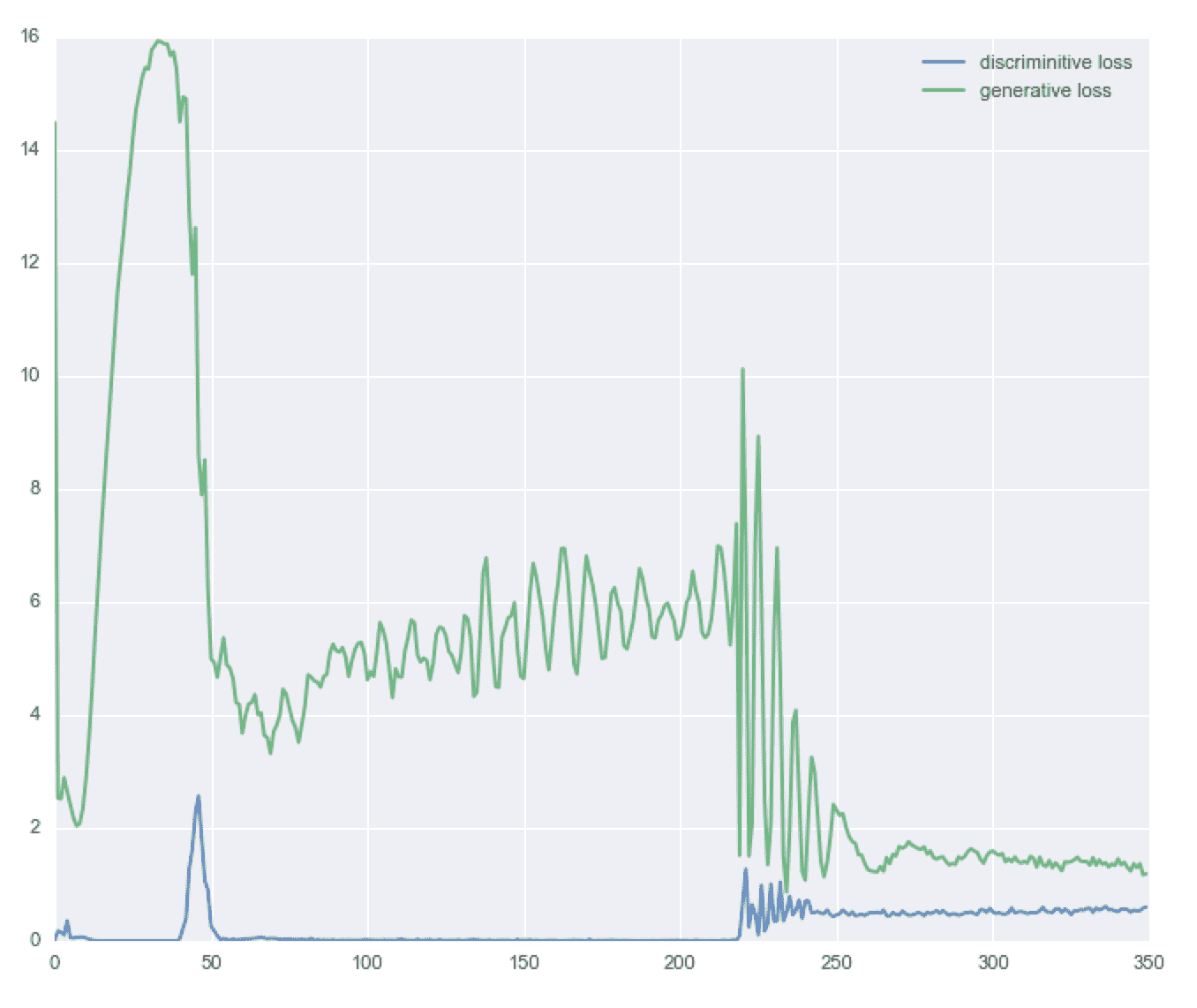 下圖提供了雙方的示例：  生成器和鑒別器的收斂示例 # 一些很酷的 GAN 應用 我們已經確定生成器學習如何偽造數據。 這意味著它將學習如何創建由網絡創建的新合成數據，并且*看起來是*真實的并且由人類創建。 在討論有關 GAN 代碼的詳細信息之前，我想分享使用 GAN 的最新論文（[代碼可在線獲得](https://github.com/hanzhanggit/StackGAN)）的結果。 從文本描述開始合成偽造的圖像。 結果令人印象深刻。 第一列是測試集中的真實圖像，其他所有列都是從 StackGAN 的 Stage-I 和 Stage-II 中相同的文本描述生成的圖像。 [YouTube 上有更多示例](https://www.youtube.com/watch?v=SuRyL5vhCIM&feature=youtu.be)：   現在，讓我們看看 GAN 如何學習**偽造** MNIST 數據集。 在這種情況下，它是用于生成器和鑒別器網絡的 GAN 和卷積網絡的組合。 最初，生成器不會產生任何可理解的東西，但是經過幾次迭代，合成的偽造數字變得越來越清晰。 在下圖中，通過增加訓練時期來對面板進行排序，您可以看到面板之間的質量改進：  改進后的圖像如下：  我們可以在下圖中看到進一步的改進：  GAN 最酷的用途之一是對生成器向量`Z`的面部進行算術。換句話說，如果我們停留在合成偽造圖像的空間中，則可能會看到類似以下內容：`[微笑的女人]-[中性的女人] + [中性的男人] = [微笑的男人]`，或類似這樣：`[戴眼鏡的男人] - [戴眼鏡的男人] + [戴眼鏡的女人] = [戴眼鏡的女人]`。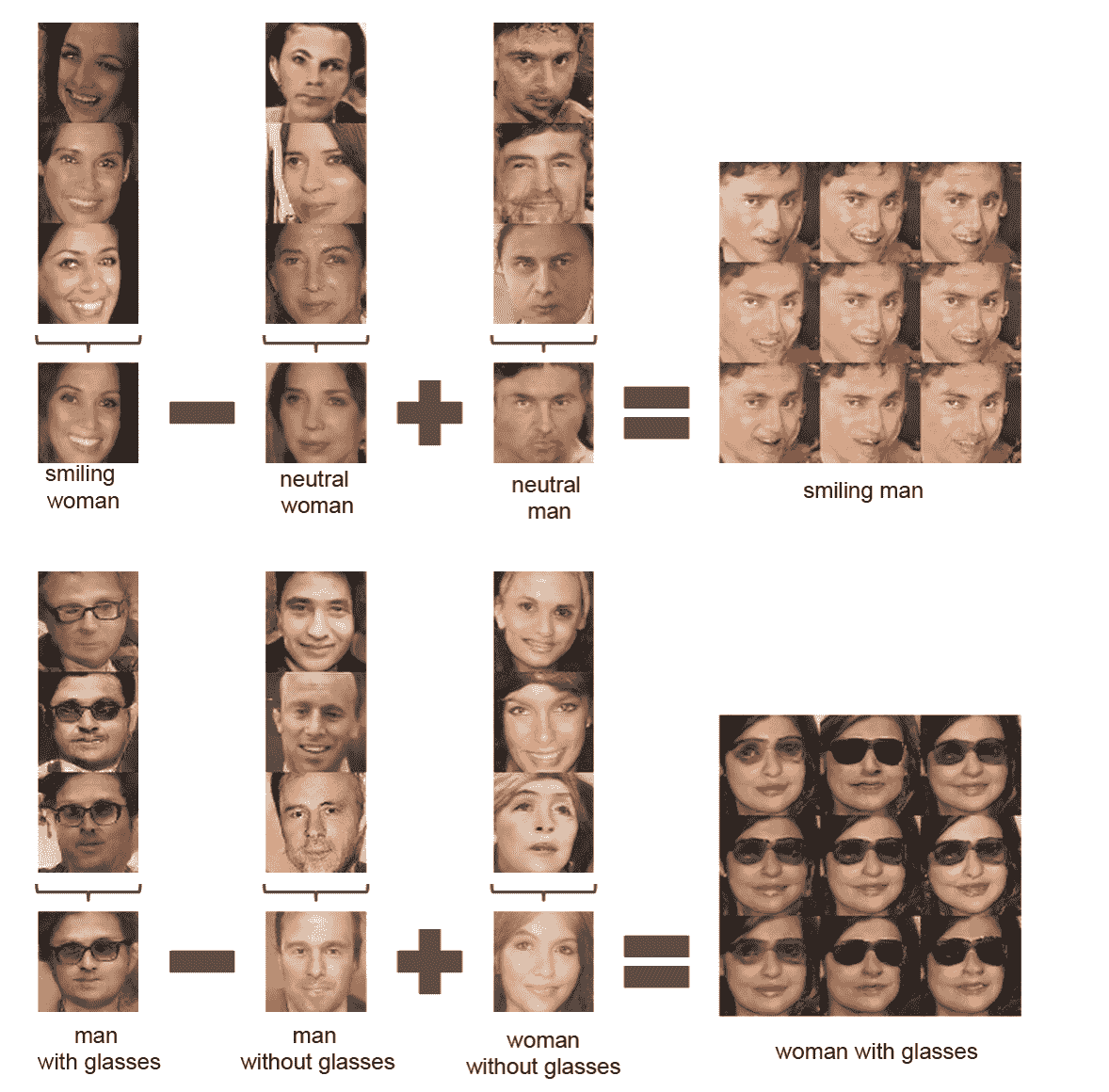 下圖取自：[《深度卷積生成對抗網絡的無監督表示學習》](https://arxiv.org/abs/1511.06434)（Alec Radford，Luke Metz，Soumith Chintala，2016）  [這個鏈接](https://github.com/Newmu/dcgan_code)提供了 GAN 的其他出色示例。 本文中所有圖像均由神經網絡生成。 他們不是真實的。 [全文可在此處找到](http://arxiv.org/abs/1511.06434)。 **臥室**：經過五個時期的訓練后生成的臥室：  生成臥室的示例 **專輯封面**：這些圖像不是真實的，而是由 GAN 生成的。 專輯封面看起來很真實：  生成專輯封面的示例 # 學習使用簡單的 GAN 偽造 MNIST 圖像 Ian J.Goodfellow，Jean Pouget-Abadie，Mehdi Mirza，Bing Xu，David Warde-Farley，Sherjil Ozair，Aaron Courville，Yoshua Bengio 等人撰寫的 Generative Adversarial Networks（2014）是更好地理解 GAN 的好論文。 在本秘籍中，我們將學習如何使用以 Generator-Discriminator 架構組織的全連接層網絡來偽造 MNIST 手寫數字。 # 準備 此秘籍基于[這個頁面](https://github.com/TengdaHan/GAN-TensorFlow)上可用的代碼。 # 操作步驟 我們按以下步驟進行： 1. 從 github 克隆代碼： ```py git clone https://github.com/TengdaHan/GAN-TensorFlow ``` 2. 定義 Xavier 初始化器，如論文`Understanding the difficulty of training deep feedforward neural networks (2009) by Xavier Glorot, Yoshua Bengio,?http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.207.2059&rep=rep1&type=pdf`中所述。事實證明，初始化器可讓 GAN 更好地收斂： ```py def xavier_init(size): in_dim = size[0] xavier_stddev = 1\. / tf.sqrt(in_dim / 2.) return xavier_stddev ``` 3. 定義輸入`X`的生成器。首先，我們定義尺寸為`[100, K = 128]`的矩陣`W1`，并根據正態分布對其進行初始化。 注意 100 是`Z`的任意值，`Z`是我們的生成器使用的初始噪聲。 然后，我們定義尺寸為`[K = 256]`的偏差`B1`。 類似地，我們定義尺寸為`[K=128, L=784]`的矩陣`W2`和尺寸為`[L = 784]`的偏置`B2`。 使用步驟 1 中定義的`xavier_init`初始化兩個矩陣`W1`和`W2`，而使用`tf.constant_initializer()`初始化`B1`和`B2`。 之后，我們計算矩陣`X * W1`之間的乘法，求和`B1`的偏差，然后將其傳遞給 RELU 激活函數以獲得`fc1`。 然后將該密集層與下一個密集層連接，該密集層是通過將矩陣`fc1`與`W2`相乘并求和`B2`的偏差而創建的。 然后將結果通過 Sigmoid 函數傳遞。 這些步驟用于定義用于生成器的兩層神經網絡： ```py def generator(X): with tf.variable_scope('generator'): K = 128 L = 784 W1 = tf.get_variable('G_W1', [100, K], initializer=tf.random_normal_initializer(stddev=xavier_init([100, K]))) B1 = tf.get_variable('G_B1', [K], initializer=tf.constant_initializer()) W2 = tf.get_variable('G_W2', [K, L], initializer=tf.random_normal_initializer(stddev=xavier_init([K, L]))) B2 = tf.get_variable('G_B2', [L], initializer=tf.constant_initializer()) # summary tf.summary.histogram('weight1', W1) tf.summary.histogram('weight2', W2) tf.summary.histogram('biases1', B1) tf.summary.histogram('biases2', B2) fc1 = tf.nn.relu((tf.matmul(X, W1) + B1)) fc2 = tf.matmul(fc1, W2) + B2 prob = tf.nn.sigmoid(fc2) return prob ``` 4. 定義輸入`X`的鑒別器。原則上，這與生成器非常相似。 主要區別在于，如果參數重用為`true`，則調用`scope.reuse_variables()`觸發重用。 然后我們定義兩個密集層。 第一層使用尺寸為`[J=784, K=128]`的矩陣`W1`，尺寸為`[K=128]`的偏差`B1`，并且它基于`X`與`W1`的標準乘積。 將該結果添加到`B1`并傳遞給 RELU 激活函數以獲取結果`fc1`。 第二個矩陣使用尺寸為`[K=128, L=1]`的矩陣`W2`和尺寸為`[L=1]`的偏差`B2`，它基于`fc1`與`W2`的標準乘積。 將此結果添加到`B2`并傳遞給 Sigmoid 函數： ```py def discriminator(X, reuse=False): with tf.variable_scope('discriminator'): if reuse: tf.get_variable_scope().reuse_variables() J = 784 K = 128 L = 1 W1 = tf.get_variable('D_W1', [J, K], initializer=tf.random_normal_initializer(stddev=xavier_init([J, K]))) B1 = tf.get_variable('D_B1', [K], initializer=tf.constant_initializer()) W2 = tf.get_variable('D_W2', [K, L], initializer=tf.random_normal_initializer(stddev=xavier_init([K, L]))) B2 = tf.get_variable('D_B2', [L], initializer=tf.constant_initializer()) # summary tf.summary.histogram('weight1', W1) tf.summary.histogram('weight2', W2) tf.summary.histogram('biases1', B1) tf.summary.histogram('biases2', B2) fc1 = tf.nn.relu((tf.matmul(X, W1) + B1)) logits = tf.matmul(fc1, W2) + B2 prob = tf.nn.sigmoid(logits) return prob, logits ``` 5. 現在讓我們定義一些有用的附加函數。 首先，我們導入一堆標準模塊： ```py import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import matplotlib.gridspec as gridspec import os import argparse ``` 6. 然后，我們從 MNIST 數據集中讀取數據，并定義了用于繪制樣本的輔助函數： ```py def read_data(): from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("../MNIST_data/", one_hot=True) return mnist def plot(samples): fig = plt.figure(figsize=(8, 8)) gs = gridspec.GridSpec(8, 8) gs.update(wspace=0.05, hspace=0.05) for i, sample in enumerate(samples): ax = plt.subplot(gs[i]) plt.axis('off') ax.set_xticklabels([]) ax.set_yticklabels([]) ax.set_aspect('equal') plt.imshow(sample.reshape(28, 28), cmap='Greys_r') return fig ``` 7. 現在讓我們定義訓練函數。 首先，讓我們讀取 MNIST 數據，然后定義一個具有一個用于標準 MNIST 手寫字符的通道的`28 x 28`形狀的矩陣`X`。 然后，讓我們定義大小為 100 的`z`噪聲向量，這是 GAN 論文中提出的一個常見選擇。 下一步是在`z`上調用生成器，然后將結果分配給`G`。之后，我們將`X`傳遞給鑒別器，而無需重用。 然后，我們將偽造/偽造的`G`結果傳遞給鑒別器，從而重用學習到的權重。 這方面的一個重要方面是我們如何選擇鑒別器的損失函數，該函數是兩個交叉熵的和：一個交叉熵，一個用于實字符，其中所有真實 MNIST 字符的標簽都設置為一個，另一個用于偽造的字符，其中所有偽造的字符的標簽都設置為零。 鑒別器和生成器以交替順序運行 100,000 步。 每 500 步，會從學習到的分布中抽取一個樣本，以打印該生成器到目前為止所學的內容。 這就是定義新周期的條件，結果將在下一節中顯示。 讓我們看看實現我們剛剛描述的代碼片段。 ```py def train(logdir, batch_size): from model_fc import discriminator, generator mnist = read_data() with tf.variable_scope('placeholder'): # Raw image X = tf.placeholder(tf.float32, [None, 784]) tf.summary.image('raw image', tf.reshape(X, [-1, 28, 28, 1]), 3) # Noise z = tf.placeholder(tf.float32, [None, 100]) # noise tf.summary.histogram('Noise', z) with tf.variable_scope('GAN'): G = generator(z) D_real, D_real_logits = discriminator(X, reuse=False) D_fake, D_fake_logits = discriminator(G, reuse=True) tf.summary.image('generated image', tf.reshape(G, [-1, 28, 28, 1]), 3) with tf.variable_scope('Prediction'): tf.summary.histogram('real', D_real) tf.summary.histogram('fake', D_fake) with tf.variable_scope('D_loss'): d_loss_real = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits( logits=D_real_logits, labels=tf.ones_like(D_real_logits))) d_loss_fake = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits( logits=D_fake_logits, labels=tf.zeros_like(D_fake_logits))) d_loss = d_loss_real + d_loss_fake tf.summary.scalar('d_loss_real', d_loss_real) tf.summary.scalar('d_loss_fake', d_loss_fake) tf.summary.scalar('d_loss', d_loss) with tf.name_scope('G_loss'): g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits (logits=D_fake_logits, labels=tf.ones_like(D_fake_logits))) tf.summary.scalar('g_loss', g_loss) tvar = tf.trainable_variables() dvar = [var for var in tvar if 'discriminator' in var.name] gvar = [var for var in tvar if 'generator' in var.name] with tf.name_scope('train'): d_train_step = tf.train.AdamOptimizer().minimize(d_loss, var_list=dvar) g_train_step = tf.train.AdamOptimizer().minimize(g_loss, var_list=gvar) sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) merged_summary = tf.summary.merge_all() writer = tf.summary.FileWriter('tmp/mnist/'+logdir) writer.add_graph(sess.graph) num_img = 0 if not os.path.exists('output/'): os.makedirs('output/') for i in range(100000): batch_X, _ = mnist.train.next_batch(batch_size) batch_noise = np.random.uniform(-1., 1., [batch_size, 100]) if i % 500 == 0: samples = sess.run(G, feed_dict={z: np.random.uniform(-1., 1., [64, 100])}) fig = plot(samples) plt.savefig('output/%s.png' % str(num_img).zfill(3), bbox_inches='tight') num_img += 1 plt.close(fig) _, d_loss_print = sess.run([d_train_step, d_loss], feed_dict={X: batch_X, z: batch_noise}) _, g_loss_print = sess.run([g_train_step, g_loss], feed_dict={z: batch_noise}) if i % 100 == 0: s = sess.run(merged_summary, feed_dict={X: batch_X, z: batch_noise}) writer.add_summary(s, i) print('epoch:%d g_loss:%f d_loss:%f' % (i, g_loss_print, d_loss_print)) if __name__ == '__main__': parser = argparse.ArgumentParser(description='Train vanila GAN using fully-connected layers networks') parser.add_argument('--logdir', type=str, default='1', help='logdir for Tensorboard, give a string') parser.add_argument('--batch_size', type=int, default=64, help='batch size: give a int') args = parser.parse_args() train(logdir=args.logdir, batch_size=args.batch_size) ``` # 工作原理 在每個時期，生成器都會進行許多預測（它會生成偽造的 MNIST 圖像），鑒別器會在將預測與實際 MNIST 圖像混合后嘗試學習如何生成偽造的圖像。 在 32 個周期之后，生成器學習偽造這組手寫數字。 沒有人對機器進行編程來編寫，但是它學會了如何編寫與人類所寫的數字沒有區別的數字。 請注意，訓練 GAN 可能非常困難，因為有必要在兩個參與者之間找到平衡。 如果您對該主題感興趣，我建議您看看[從業者收集的一系列技巧](https://github.com/soumith/ganhacks)。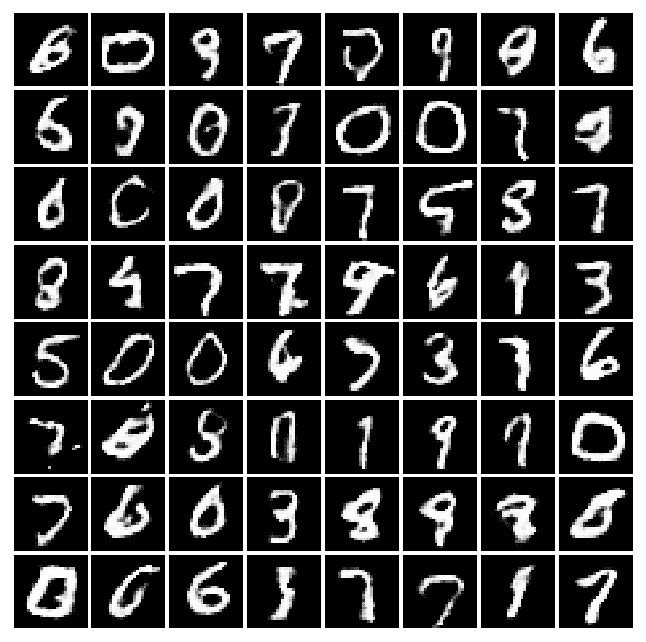 讓我們看一下不同時期的許多實際示例，以了解機器將如何學習以改善其編寫過程： | | | | | --- | --- | --- | |  |  |  | | 周期 0 | 周期 2 | 周期 4 | |  |  |  | | 周期 8 | 周期 16 | 周期 32 | |  |  | 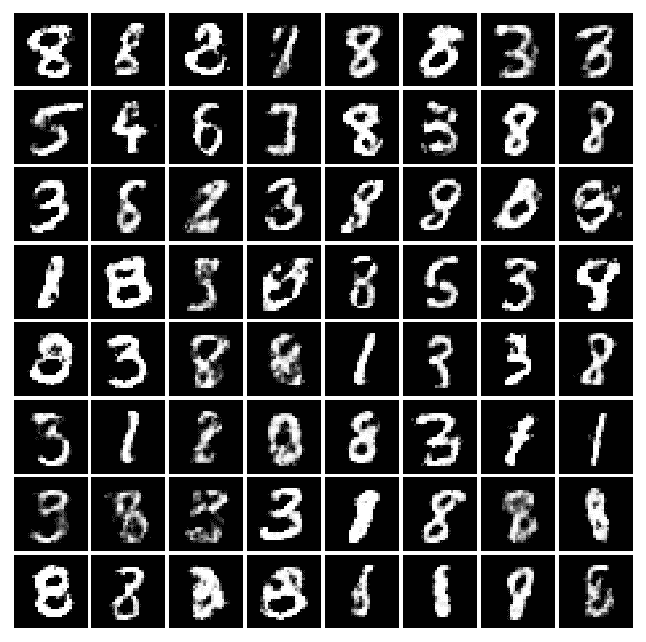 | | 周期 64 | 周期 128 | 周期 200 | Example of forged MNIST-like characters with a GAN # 學習使用 DCGAN 偽造 MNIST 圖像 在本秘籍中，我們將使用一個簡單的 GAN，它使用 CNN 來學習如何偽造 MNIST 圖像并創建不屬于原始數據集的新圖像。 這個想法是 CNN 與 GAN 一起使用將提高處理圖像數據集的能力。 請注意，先前的方法是將 GAN 與完全連接的網絡一起使用，而在此我們重點介紹 CNN。 # 準備 此秘籍基于[這個頁面](https://github.com/TengdaHan/GAN-TensorFlow)上可用的代碼。 # 操作步驟 我們按以下步驟進行： 1. 從 github 克隆代碼： ```py git clone https://github.com/TengdaHan/GAN-TensorFlow ``` 2. 定義 Xavier 初始化器，如論文`Understanding the difficulty of training deep feedforward neural networks (2009) by Xavier Glorot, Yoshua Bengio,?http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.207.2059&rep=rep1&type=pdf`中所述。事實證明，初始化器可讓 GAN 更好地收斂： ```py def xavier_init(size): in_dim = size[0] xavier_stddev = 1\. / tf.sqrt(in_dim / 2.) # return tf.random_normal(shape=size, stddev=xavier_stddev) return xavier_stddev ``` 3. 為給定輸入`x`，權重`w`，偏差`b`和給定*步幅*定義卷積運算。 我們的代碼使用標準的`tf.nn.conv2d(...)`模塊。 請注意，我們使用第 4 章中定義的`SAME`填充： ```py def conv(x, w, b, stride, name): with tf.variable_scope('conv'): tf.summary.histogram('weight', w) tf.summary.histogram('biases', b) return tf.nn.conv2d(x, filter=w, strides=[1, stride, stride, 1], padding='SAME', name=name) + b ``` 4. 為給定輸入`x`，權重`w`，偏差`b`和給定*步幅*定義反卷積運算。 我們的代碼使用標準的`tf.nn.conv2d_transpose(...)`模塊。 同樣，我們使用`'SAME'`填充。 ```py def deconv(x, w, b, shape, stride, name): with tf.variable_scope('deconv'): tf.summary.histogram('weight', w) tf.summary.histogram('biases', b) return tf.nn.conv2d_transpose(x, filter=w, output_shape=shape, strides=[1, stride, stride, 1], padding='SAME', name=name) + b ``` 5. 定義一個標準`LeakyReLU`，這對于 GAN 是非常有效的激活函數： ```py def lrelu(x, alpha=0.2): with tf.variable_scope('leakyReLU'): return tf.maximum(x, alpha * x) ``` 6. 定義生成器。 首先，我們定義輸入大小為 100（Z 的任意大小，即生成器使用的初始噪聲）的完全連接層。 全連接層由尺寸為`[100, 7 * 7 * 256]`且根據正態分布初始化的矩陣`W1`和尺寸為`[7 * 7 * 256]`的偏置`B1`組成。 該層使用 ReLu 作為激活函數。 在完全連接的層之后，生成器將應用兩個反卷積運算 deconv1 和 deconv2，兩者的步幅均為 2。 完成第一個 deconv1 操作后，將結果批量標準化。 請注意，第二次反卷積運算之前會出現丟棄，概率為 40%。 最后一個階段是一個 Sigmoid，用作非線性激活，如下面的代碼片段所示： ```py def generator(X, batch_size=64): with tf.variable_scope('generator'): K = 256 L = 128 M = 64 W1 = tf.get_variable('G_W1', [100, 7*7*K], initializer=tf.random_normal_initializer(stddev=0.1)) B1 = tf.get_variable('G_B1', [7*7*K], initializer=tf.constant_initializer()) W2 = tf.get_variable('G_W2', [4, 4, M, K], initializer=tf.random_normal_initializer(stddev=0.1)) B2 = tf.get_variable('G_B2', [M], initializer=tf.constant_initializer()) W3 = tf.get_variable('G_W3', [4, 4, 1, M], initializer=tf.random_normal_initializer(stddev=0.1)) B3 = tf.get_variable('G_B3', [1], initializer=tf.constant_initializer()) X = lrelu(tf.matmul(X, W1) + B1) X = tf.reshape(X, [batch_size, 7, 7, K]) deconv1 = deconv(X, W2, B2, shape=[batch_size, 14, 14, M], stride=2, name='deconv1') bn1 = tf.contrib.layers.batch_norm(deconv1) deconv2 = deconv(tf.nn.dropout(lrelu(bn1), 0.4), W3, B3, shape=[batch_size, 28, 28, 1], stride=2, name='deconv2') XX = tf.reshape(deconv2, [-1, 28*28], 'reshape') return tf.nn.sigmoid(XX) ``` 7. 定義鑒別器。 與前面的秘籍一樣，如果參數重用為`true`，則調用`scope.reuse_variables()`觸發重用。 鑒別器使用兩個卷積層。 第一個是批量歸一化，而第二個是概率為 40% 的丟棄，然后是批量歸一化步驟。 之后，我們得到了一個具有激活函數 ReLU 的致密層，然后是另一個具有基于 Sigmoid 激活函數的致密層： ```py def discriminator(X, reuse=False): with tf.variable_scope('discriminator'): if reuse: tf.get_variable_scope().reuse_variables() K = 64 M = 128 N = 256 W1 = tf.get_variable('D_W1', [4, 4, 1, K], initializer=tf.random_normal_initializer(stddev=0.1)) B1 = tf.get_variable('D_B1', [K], initializer=tf.constant_initializer()) W2 = tf.get_variable('D_W2', [4, 4, K, M], initializer=tf.random_normal_initializer(stddev=0.1)) B2 = tf.get_variable('D_B2', [M], initializer=tf.constant_initializer()) W3 = tf.get_variable('D_W3', [7*7*M, N], initializer=tf.random_normal_initializer(stddev=0.1)) B3 = tf.get_variable('D_B3', [N], initializer=tf.constant_initializer()) W4 = tf.get_variable('D_W4', [N, 1], initializer=tf.random_normal_initializer(stddev=0.1)) B4 = tf.get_variable('D_B4', [1], initializer=tf.constant_initializer()) X = tf.reshape(X, [-1, 28, 28, 1], 'reshape') conv1 = conv(X, W1, B1, stride=2, name='conv1') bn1 = tf.contrib.layers.batch_norm(conv1) conv2 = conv(tf.nn.dropout(lrelu(bn1), 0.4), W2, B2, stride=2, name='conv2') bn2 = tf.contrib.layers.batch_norm(conv2) flat = tf.reshape(tf.nn.dropout(lrelu(bn2), 0.4), [-1, 7*7*M], name='flat') dense = lrelu(tf.matmul(flat, W3) + B3) logits = tf.matmul(dense, W4) + B4 prob = tf.nn.sigmoid(logits) return prob, logits ``` 8. 然后，我們從 MNIST 數據集中讀取數據，并定義用于繪制樣本的輔助函數： ```py import numpy as np import matplotlib.pyplot as plt import matplotlib.gridspec as gridspec import os import argparse def read_data(): from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("../MNIST_data/", one_hot=True) return mnist def plot(samples): fig = plt.figure(figsize=(8, 8)) gs = gridspec.GridSpec(8, 8) gs.update(wspace=0.05, hspace=0.05) for i, sample in enumerate(samples): ax = plt.subplot(gs[i]) plt.axis('off') ax.set_xticklabels([]) ax.set_yticklabels([]) ax.set_aspect('equal') plt.imshow(sample.reshape(28, 28), cmap='Greys_r') return fig ``` 9. 現在讓我們定義訓練函數。 首先，讓我們讀取 MNIST 數據，然后定義一個具有一個用于標準 MNIST 手寫字符的通道的`28 x 28`形狀的矩陣`X`。 然后，讓我們定義大小為 100 的`z`噪聲向量，這是 GAN 論文中提出的一個常見選擇。 下一步是在`z`上調用生成器，然后將結果分配給`G`。之后，我們將`X`傳遞給鑒別器，而無需重用。 然后，我們將偽造/偽造的`G`結果傳遞給鑒別器，從而重用學習到的權重。 這方面的一個重要方面是我們如何選擇鑒別函數的損失函數，該函數是兩個交叉熵的和：一個用于實字符，其中所有真實 MNIST 字符的標號都設置為 1，一個用于遺忘字符，其中所有偽造的字符的標簽設置為零。 鑒別器和生成器以交替順序運行 100,000 步。 每 500 步，會從學習到的分布中抽取一個樣本，以打印該生成器到目前為止所學的內容。 這就是定義新周期的條件，結果將在下一部分中顯示。 訓練函數代碼段報告如下 ```py def train(logdir, batch_size): from model_conv import discriminator, generator mnist = read_data() with tf.variable_scope('placeholder'): # Raw image X = tf.placeholder(tf.float32, [None, 784]) tf.summary.image('raw image', tf.reshape(X, [-1, 28, 28, 1]), 3) # Noise z = tf.placeholder(tf.float32, [None, 100]) # noise tf.summary.histogram('Noise', z) with tf.variable_scope('GAN'): G = generator(z, batch_size) D_real, D_real_logits = discriminator(X, reuse=False) D_fake, D_fake_logits = discriminator(G, reuse=True) tf.summary.image('generated image', tf.reshape(G, [-1, 28, 28, 1]), 3) with tf.variable_scope('Prediction'): tf.summary.histogram('real', D_real) tf.summary.histogram('fake', D_fake) with tf.variable_scope('D_loss'): d_loss_real = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits( logits=D_real_logits, labels=tf.ones_like(D_real_logits))) d_loss_fake = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits( logits=D_fake_logits, labels=tf.zeros_like(D_fake_logits))) d_loss = d_loss_real + d_loss_fake tf.summary.scalar('d_loss_real', d_loss_real) tf.summary.scalar('d_loss_fake', d_loss_fake) tf.summary.scalar('d_loss', d_loss) with tf.name_scope('G_loss'): g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits (logits=D_fake_logits, labels=tf.ones_like(D_fake_logits))) tf.summary.scalar('g_loss', g_loss) tvar = tf.trainable_variables() dvar = [var for var in tvar if 'discriminator' in var.name] gvar = [var for var in tvar if 'generator' in var.name] with tf.name_scope('train'): d_train_step = tf.train.AdamOptimizer().minimize(d_loss, var_list=dvar) g_train_step = tf.train.AdamOptimizer().minimize(g_loss, var_list=gvar) sess = tf.Session() init = tf.global_variables_initializer() sess.run(init) merged_summary = tf.summary.merge_all() writer = tf.summary.FileWriter('tmp/'+'gan_conv_'+logdir) writer.add_graph(sess.graph) num_img = 0 if not os.path.exists('output/'): os.makedirs('output/') for i in range(100000): batch_X, _ = mnist.train.next_batch(batch_size) batch_noise = np.random.uniform(-1., 1., [batch_size, 100]) if i % 500 == 0: samples = sess.run(G, feed_dict={z: np.random.uniform(-1., 1., [64, 100])}) fig = plot(samples) plt.savefig('output/%s.png' % str(num_img).zfill(3), bbox_inches='tight') num_img += 1 plt.close(fig) _, d_loss_print = sess.run([d_train_step, d_loss], feed_dict={X: batch_X, z: batch_noise}) _, g_loss_print = sess.run([g_train_step, g_loss], feed_dict={z: batch_noise}) if i % 100 == 0: s = sess.run(merged_summary, feed_dict={X: batch_X, z: batch_noise}) writer.add_summary(s, i) print('epoch:%d g_loss:%f d_loss:%f' % (i, g_loss_print, d_loss_print)) if __name__ == '__main__': parser = argparse.ArgumentParser(description='Train vanila GAN using convolutional networks') parser.add_argument('--logdir', type=str, default='1', help='logdir for Tensorboard, give a string') parser.add_argument('--batch_size', type=int, default=64, help='batch size: give a int') args = parser.parse_args() train(logdir=args.logdir, batch_size=args.batch_size) ``` # 工作原理 將 CNN 與 GAN 一起使用可提高學習能力。 讓我們看一下不同時期的許多實際示例，以了解機器將如何學習以改善其編寫過程。 例如，將以下秘籍中的四次迭代后獲得的結果與先前秘籍中的四次迭代后獲得的結果進行比較。 你看得到差別嗎？ 我希望自己可以學習這種藝術！ | | | | | --- | --- | --- | |  |  |  | | 周期 0 | 周期 2 | 周期 4 | |  |  |  | | 周期 8 | 周期 16 | 周期 32 | |  | 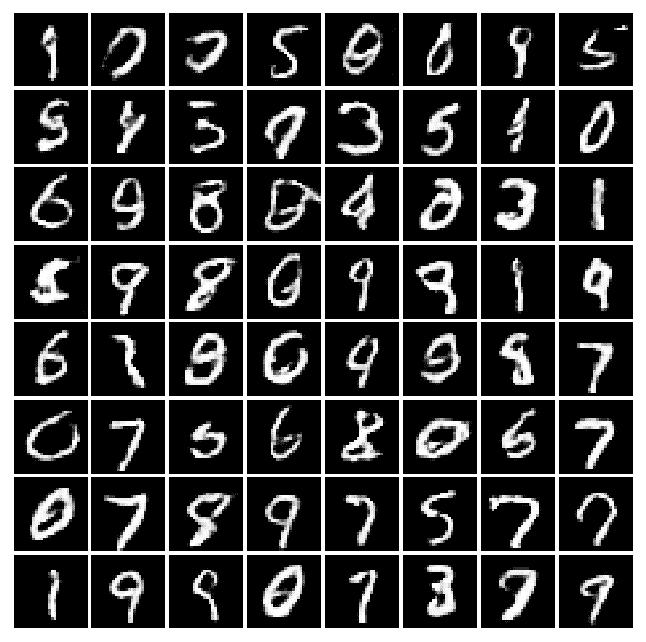 | 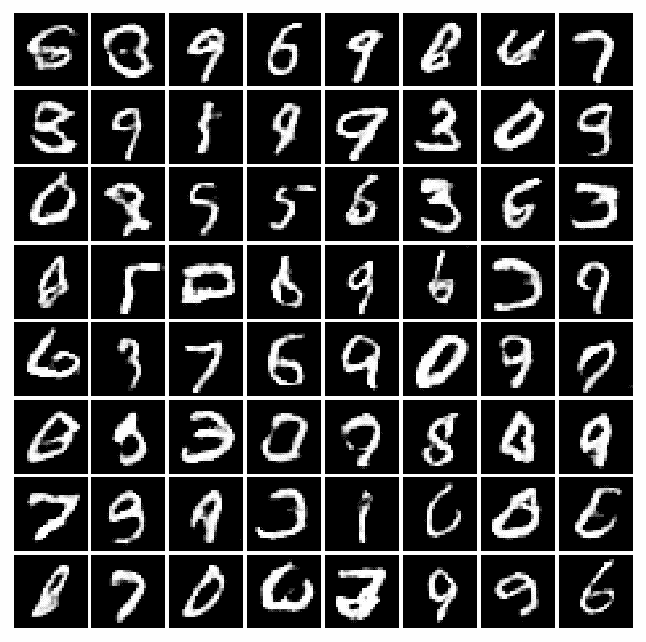 | | 周期 64 | 周期 128 | 周期 200 | Example of forged MNIST-like with DCGAN # 學習使用 DCGAN 偽造名人人臉和其他數據集 用于偽造 MNIST 圖像的相同思想可以應用于其他圖像域。 在本秘籍中，您將學習如何使用位于[這個鏈接](https://github.com/carpedm20/DCGAN-tensorflow)的包在不同的數據集上訓練 DCGAN 模型。 這項工作基于論文《深度卷積生成對抗網絡的無監督表示學習》（Alec Radford，Luke Metz，Soumith Chintal，2015 年）。引用摘要： 近年來，通過卷積網絡（CNN）進行監督學習已在計算機視覺應用中得到了廣泛采用。 相比之下，CNN 的無監督學習受到的關注較少。 在這項工作中，我們希望幫助彌合CNN在有監督學習的成功與無監督學習之間的差距。 我們介紹了一種稱為深度卷積生成對抗網絡（DCGAN）的 CNN，它們具有一定的架構約束，并證明它們是無監督學習的強大候選者。 在各種圖像數據集上進行訓練，我們顯示出令人信服的證據，即我們深厚的卷積對抗對在生成器和鑒別器中學習了從對象部分到場景的表示層次。 此外，我們將學習到的特征用于新穎的任務-展示了它們作為一般圖像表示形式的適用性。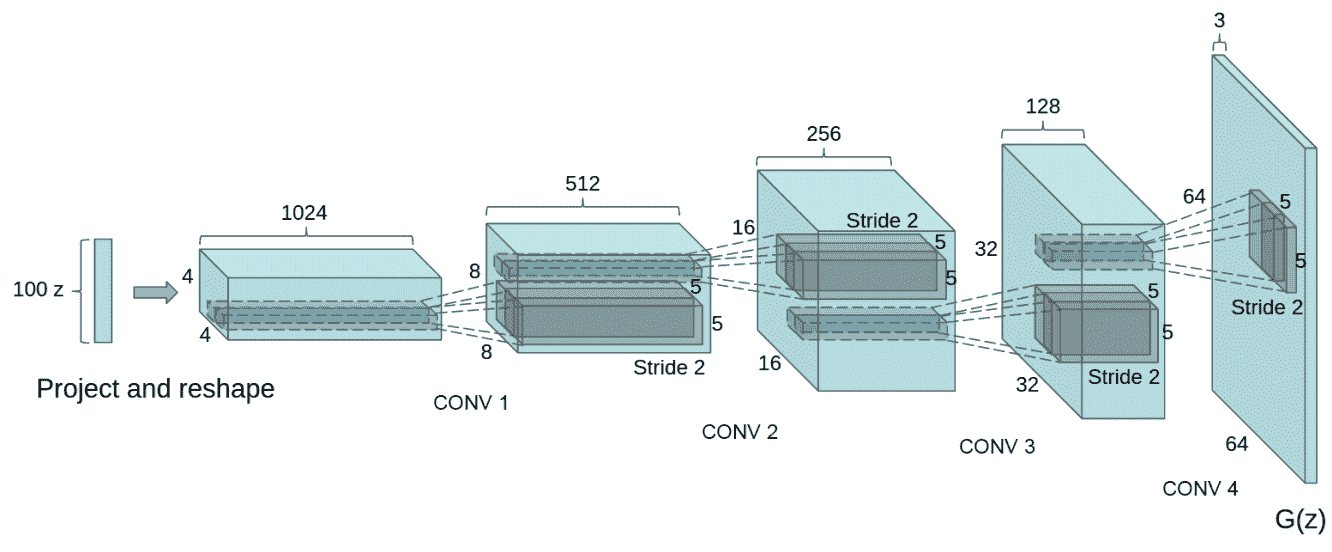 請注意，生成器具有下圖所示的架構：  請注意，在包裝中，相對于原始紙張進行了更改，以避免`D`（鑒別器）網絡快速收斂，`G`（生成器）網絡每次`D`網絡更新都會更新兩次。 # 準備 此秘籍基于[這個頁面](https://github.com/carpedm20/DCGAN-tensorflow)上提供的代碼。 # 操作步驟 我們按以下步驟進行： 1. 從 Github 克隆代碼： ```py git clone https://github.com/carpedm20/DCGAN-tensorflow ``` 2. 使用以下命令下載數據集： ```py python download.py mnist celebA ``` 3. 要使用下載的數據集訓練模型，請使用以下命令： ```py python main.py --dataset celebA --input_height=108 --train --crop ``` 4. 要使用現有模型對其進行測試，請使用以下命令： ```py python main.py --dataset celebA --input_height=108 --crop ``` 5. 另外，您可以通過執行以下操作來使用自己的數據集： ```py $ mkdir data/DATASET_NAME ... add images to data/DATASET_NAME ... $ python main.py --dataset DATASET_NAME --train $ python main.py --dataset DATASET_NAME $ # example $ python main.py --dataset=eyes --input_fname_pattern="*_cropped.png" --train ``` # 工作原理 生成器學習如何生成名人的偽造圖像，鑒別器學習如何將偽造的圖像與真實的圖像區分開。 兩個網絡中的每個周期都在競爭以改善和減少損失。 下表報告了前五個時期： | | | | --- | --- | |  |  | | 周期 0 | 周期 1 | |  |  | | 周期 2 | 周期 3 | |  |  | | 周期 4 | 周期 5 | Example of forged celebrities with a DCGAN # 更多 內容感知填充是攝影師使用的一種工具，用于填充不需要的或丟失的圖像部分。論文[《具有感知和上下文損失的語義圖像修復》](https://arxiv.org/abs/1607.07539)使用 DCGAN 進行圖像補全，并學習如何填充部分圖像。 # 實現變分自編碼器 **變分自編碼器**（**VAE**）是神經網絡和貝葉斯推理兩者的最佳結合。 它們是最酷的神經網絡，并已成為無監督學習的流行方法之一。 它們是自編碼器。 與傳統的編碼器和自編碼器的解碼器網絡（請參閱第 8 章“自編碼器”）一起，它們還具有其他隨機層。 編碼器網絡之后的隨機層使用高斯分布對數據進行采樣，解碼器網絡之后的隨機層使用伯努利分布對數據進行采樣。 像 GAN 一樣，可以使用變分自編碼器根據經過訓練的分布來生成圖像和圖形。 VAE 允許人們設置潛在的復雜先驗，從而學習強大的潛在表示。 下圖描述了 VAE。 編碼器網絡`q?(z | x)`逼近真實但棘手的后驗分布`p(z | x)`，其中`x`是 VAE 的輸入，`z`是潛在表示。 解碼器網絡`p[?](x | z)`將`d`維潛在變量（也稱為潛在空間）作為其輸入，并且分布與`P(x)`相同。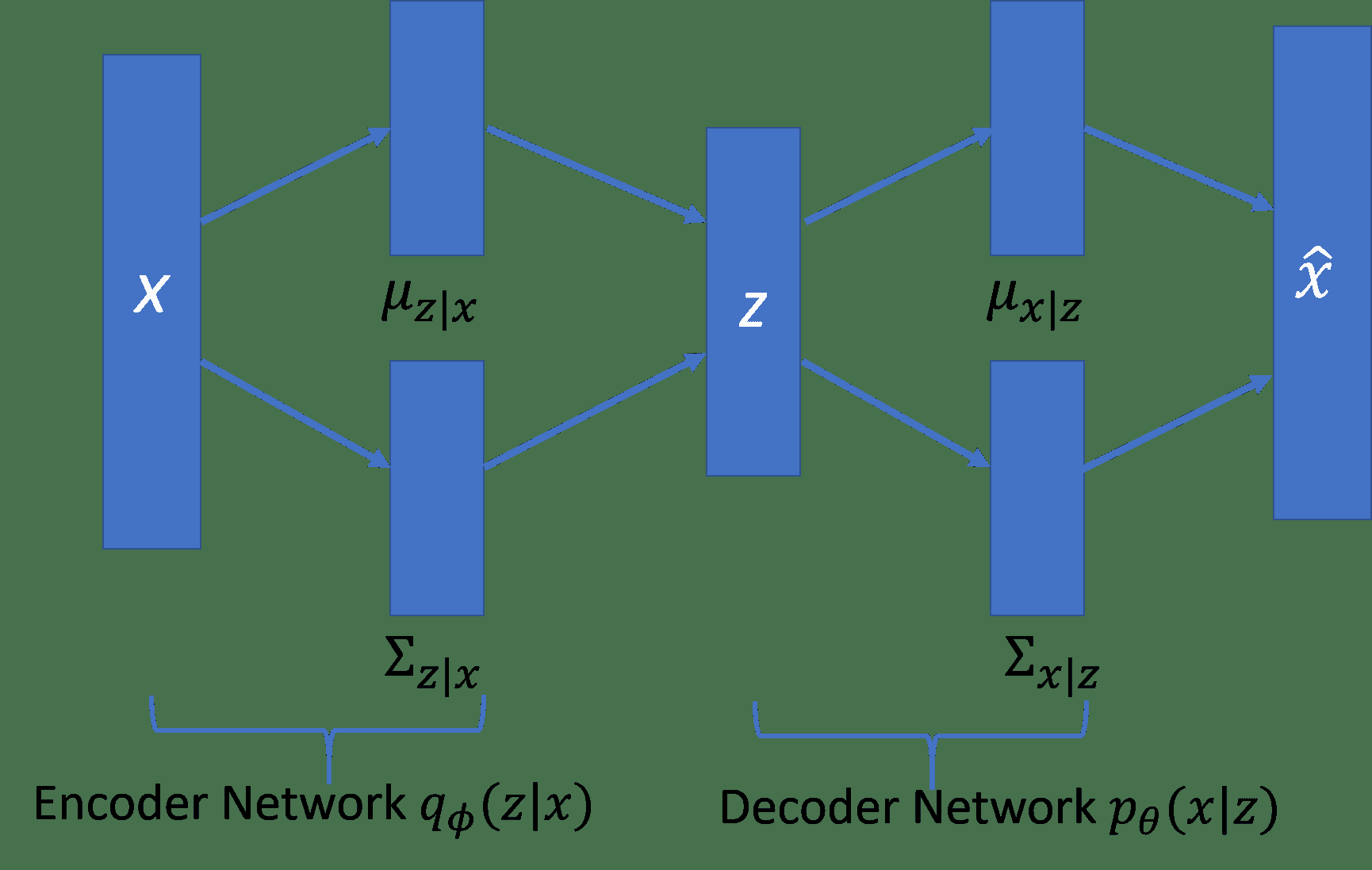 從`z | x ~ N(μ[z|x], Σ[z|x])`中采樣潛在表示`z`，解碼器網絡的輸出從`x | z ~ N(μ[x|z], Σ[x|z])`中采樣`x | z`：  自動編碼器的編碼器-解碼器示例。 # 準備 既然我們已經掌握了 VAE 的基本架構，那么就出現了一個問題，即如何對它們進行訓練，因為訓練數據的最大可能性和后驗密度是很難解決的？ 通過最大化日志數據可能性的下限來訓練網絡。 因此，損耗項包括兩個部分：生成損耗，它是通過解碼器網絡通過采樣獲得的；以及 KL 發散項，也稱為潛在損耗。 生成損失確保解碼器生成的圖像和用于訓練網絡的圖像相同，而潛在損失確保后驗分布`q?(z | x)`接近先前的`p[?](z)`。 由于編碼器使用高斯分布進行采樣，因此潛在損失可以衡量潛在變量與單位高斯的匹配程度。 對 VAE 進行訓練后，我們只能使用解碼器網絡來生成新圖像。 # 操作步驟 此處的代碼基于 Kingma 和 Welling 的論文[自動編碼變分貝葉斯](https://arxiv.org/pdf/1312.6114.pdf)，并改編自 [GitHub](https://jmetzen.github.io/2015-11-27/vae.html)。 1. 第一步是始終導入必要的模塊。 對于此秘籍，我們將需要 Numpy，Matplolib 和 TensorFlow： ```py import numpy as np import tensorflow as tf import matplotlib.pyplot as plt %matplotlib inline ``` 2. 接下來，我們定義`VariationalAutoencoder`類。 `class __init__ method`定義了超參數，例如學習率，批量大小，輸入的占位符以及編碼器和解碼器網絡的權重和偏差變量。 它還根據 VAE 的網絡架構構建計算圖。 在此秘籍中，我們使用 Xavier 初始化來初始化權重。 我們沒有定義自己的 Xavier 初始化方法，而是使用`tf.contrib.layers.xavier_initializer()` TensorFlow 來完成任務。 最后，我們定義損失（生成和潛在）和優化器操作： ```py class VariationalAutoencoder(object): def __init__(self, network_architecture, transfer_fct=tf.nn.softplus, learning_rate=0.001, batch_size=100): self.network_architecture = network_architecture self.transfer_fct = transfer_fct self.learning_rate = learning_rate self.batch_size = batch_size # Place holder for the input self.x = tf.placeholder(tf.float32, [None, network_architecture["n_input"]]) # Define weights and biases network_weights = self._initialize_weights(**self.network_architecture) # Create autoencoder network # Use Encoder Network to determine mean and # (log) variance of Gaussian distribution in latent # space self.z_mean, self.z_log_sigma_sq = \ self._encoder_network(network_weights["weights_encoder"], network_weights["biases_encoder"]) # Draw one sample z from Gaussian distribution n_z = self.network_architecture["n_z"] eps = tf.random_normal((self.batch_size, n_z), 0, 1, dtype=tf.float32) # z = mu + sigma*epsilon self.z = tf.add(self.z_mean,tf.multiply(tf.sqrt(tf.exp(self.z_log_sigma_sq)), eps)) # Use Decoder network to determine mean of # Bernoulli distribution of reconstructed input self.x_reconstr_mean = \ self._decoder_network(network_weights["weights_decoder"], network_weights["biases_decoder"]) # Define loss function based variational upper-bound and # corresponding optimizer # define generation loss generation_loss = \ -tf.reduce_sum(self.x * tf.log(1e-10 + self.x_reconstr_mean) + (1-self.x) * tf.log(1e-10 + 1 - self.x_reconstr_mean), 1) latent_loss = -0.5 * tf.reduce_sum(1 + self.z_log_sigma_sq - tf.square(self.z_mean)- tf.exp(self.z_log_sigma_sq), 1) self.cost = tf.reduce_mean(generation_loss + latent_loss) # average over batch # Define the optimizer self.optimizer = \ tf.train.AdamOptimizer(learning_rate=self.learning_rate).minimize(self.cost) # Initializing the tensor flow variables init = tf.global_variables_initializer() # Launch the session self.sess = tf.InteractiveSession() self.sess.run(init) def _initialize_weights(self, n_hidden_recog_1, n_hidden_recog_2, n_hidden_gener_1, n_hidden_gener_2, n_input, n_z): initializer = tf.contrib.layers.xavier_initializer() all_weights = dict() all_weights['weights_encoder'] = { 'h1': tf.Variable(initializer(shape=(n_input, n_hidden_recog_1))), 'h2': tf.Variable(initializer(shape=(n_hidden_recog_1, n_hidden_recog_2))), 'out_mean': tf.Variable(initializer(shape=(n_hidden_recog_2, n_z))), 'out_log_sigma': tf.Variable(initializer(shape=(n_hidden_recog_2, n_z)))} all_weights['biases_encoder'] = { 'b1': tf.Variable(tf.zeros([n_hidden_recog_1], dtype=tf.float32)), 'b2': tf.Variable(tf.zeros([n_hidden_recog_2], dtype=tf.float32)), 'out_mean': tf.Variable(tf.zeros([n_z], dtype=tf.float32)), 'out_log_sigma': tf.Variable(tf.zeros([n_z], dtype=tf.float32))} all_weights['weights_decoder'] = { 'h1': tf.Variable(initializer(shape=(n_z, n_hidden_gener_1))), 'h2': tf.Variable(initializer(shape=(n_hidden_gener_1, n_hidden_gener_2))), 'out_mean': tf.Variable(initializer(shape=(n_hidden_gener_2, n_input))), 'out_log_sigma': tf.Variable(initializer(shape=(n_hidden_gener_2, n_input)))} all_weights['biases_decoder'] = { 'b1': tf.Variable(tf.zeros([n_hidden_gener_1], dtype=tf.float32)), 'b2': tf.Variable(tf.zeros([n_hidden_gener_2], dtype=tf.float32)),'out_mean': tf.Variable(tf.zeros([n_input], dtype=tf.float32)), 'out_log_sigma': tf.Variable(tf.zeros([n_input], dtype=tf.float32))} return all_weights ``` 3. 我們建立編碼器網絡和解碼器網絡。 編碼器網絡的第一層正在獲取輸入并生成輸入的簡化的潛在表示。 第二層將輸入映射到高斯分布。 網絡學習了以下轉換： ```py def _encoder_network(self, weights, biases): # Generate probabilistic encoder (recognition network), which # maps inputs onto a normal distribution in latent space. # The transformation is parametrized and can be learned. layer_1 = self.transfer_fct(tf.add(tf.matmul(self.x, weights['h1']), biases['b1'])) layer_2 = self.transfer_fct(tf.add(tf.matmul(layer_1, weights['h2']), biases['b2'])) z_mean = tf.add(tf.matmul(layer_2, weights['out_mean']), biases['out_mean']) z_log_sigma_sq = \ tf.add(tf.matmul(layer_2, weights['out_log_sigma']), biases['out_log_sigma']) return (z_mean, z_log_sigma_sq) def _decoder_network(self, weights, biases): # Generate probabilistic decoder (decoder network), which # maps points in latent space onto a Bernoulli distribution in data space. # The transformation is parametrized and can be learned. layer_1 = self.transfer_fct(tf.add(tf.matmul(self.z, weights['h1']), biases['b1'])) layer_2 = self.transfer_fct(tf.add(tf.matmul(layer_1, weights['h2']), biases['b2'])) x_reconstr_mean = \ tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['out_mean']), biases['out_mean'])) return x_reconstr_mean ``` 4. `VariationalAutoencoder`類還包含一些輔助函數，用于生成和重建數據并適合 VAE： ```py def fit(self, X): opt, cost = self.sess.run((self.optimizer, self.cost), feed_dict={self.x: X}) return cost def generate(self, z_mu=None): """ Generate data by sampling from latent space. If z_mu is not None, data for this point in latent space is generated. Otherwise, z_mu is drawn from prior in latent space. """ if z_mu is None: z_mu = np.random.normal(size=self.network_architecture["n_z"]) # Note: This maps to mean of distribution, we could alternatively # sample from Gaussian distribution return self.sess.run(self.x_reconstr_mean, feed_dict={self.z: z_mu}) def reconstruct(self, X): """ Use VAE to reconstruct given data. """ return self.sess.run(self.x_reconstr_mean, feed_dict={self.x: X}) ``` 5. 一旦完成了 VAE 類，我們就定義了一個訓練函數，它使用 VAE 類對象并為給定數據訓練它。 ```py def train(network_architecture, learning_rate=0.001, batch_size=100, training_epochs=10, display_step=5): vae = VariationalAutoencoder(network_architecture, learning_rate=learning_rate, batch_size=batch_size) # Training cycle for epoch in range(training_epochs): avg_cost = 0. total_batch = int(n_samples / batch_size) # Loop over all batches for i in range(total_batch): batch_xs, _ = mnist.train.next_batch(batch_size) # Fit training using batch data cost = vae.fit(batch_xs) # Compute average loss avg_cost += cost / n_samples * batch_size # Display logs per epoch step if epoch % display_step == 0: print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost)) return vae ``` 6. 現在讓我們使用 VAE 類和訓練函數。 我們將 VAE 用于我們最喜歡的 MNIST 數據集： ```py # Load MNIST data in a format suited for tensorflow. # The script input_data is available under this URL: #https://raw.githubusercontent.com/tensorflow/tensorflow/master/tensorflow/examples/tutorials/mnist/input_data.py from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets('MNIST_data', one_hot=True) n_samples = mnist.train.num_examples ``` 7. 我們定義網絡架構，并在 MNIST 數據集上進行 VAE 訓練。 在這種情況下，為簡單起見，我們保留潛在尺寸 2。 ```py network_architecture = \ dict(n_hidden_recog_1=500, # 1st layer encoder neurons n_hidden_recog_2=500, # 2nd layer encoder neurons n_hidden_gener_1=500, # 1st layer decoder neurons n_hidden_gener_2=500, # 2nd layer decoder neurons n_input=784, # MNIST data input (img shape: 28*28) n_z=2) # dimensionality of latent space vae = train(network_architecture, training_epochs=75) ``` 8. 現在讓我們看看 VAE 是否真正重建了輸入。 輸出結果表明確實可以重建數字，并且由于我們使用了 2D 潛在空間，因此圖像明顯模糊： ```py x_sample = mnist.test.next_batch(100)[0] x_reconstruct = vae.reconstruct(x_sample) plt.figure(figsize=(8, 12)) for i in range(5): plt.subplot(5, 2, 2*i + 1) plt.imshow(x_sample[i].reshape(28, 28), vmin=0, vmax=1, cmap="gray") plt.title("Test input") plt.colorbar() plt.subplot(5, 2, 2*i + 2) plt.imshow(x_reconstruct[i].reshape(28, 28), vmin=0, vmax=1, cmap="gray") plt.title("Reconstruction") plt.colorbar() plt.tight_layout() ``` 以下是上述代碼的輸出：  MNIST 重建字符的示例 9. 以下是使用經過訓練的 VAE 生成的手寫數字示例： ```py nx = ny = 20 x_values = np.linspace(-3, 3, nx) y_values = np.linspace(-3, 3, ny) canvas = np.empty((28*ny, 28*nx)) for i, yi in enumerate(x_values): for j, xi in enumerate(y_values): z_mu = np.array([[xi, yi]]*vae.batch_size) x_mean = vae.generate(z_mu) canvas[(nx-i-1)*28:(nx-i)*28, j*28:(j+1)*28] = x_mean[0].reshape(28, 28) plt.figure(figsize=(8, 10)) Xi, Yi = np.meshgrid(x_values, y_values) plt.imshow(canvas, origin="upper", cmap="gray") plt.tight_layout() ``` 以下是自編碼器生成的 MNIST 類字符的范圍：  由自動編碼器生成的一系列 MNIST 字符 # 工作原理 VAE 學會重建并同時生成新圖像。 生成的圖像取決于潛在空間。 生成的圖像與訓練的數據集具有相同的分布。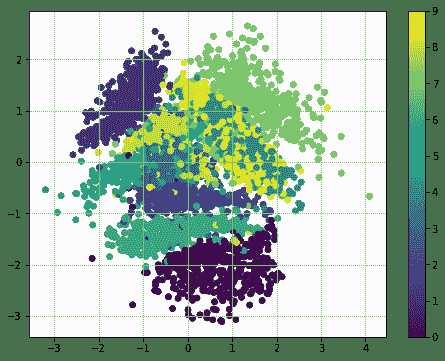 我們還可以通過在`VariationalAutoencoder`類中定義一個轉換函數來查看潛在空間中的數據： ```py def transform(self, X): """Transform data by mapping it into the latent space.""" # Note: This maps to mean of distribution, we could alternatively sample from Gaussian distribution return self.sess.run(self.z_mean, feed_dict={self.x: X}) ``` 使用轉換函數的 MNIST 數據集的潛在表示如下：  # 更多 VAE 的生成圖像取決于潛在空間尺寸。 模糊減少了潛在空間的尺寸，增加了。 分別針對 5 維，10 維和 20 維潛在維度的重構圖像如下：  # 另見 [Kingma 和 Welling 的論文](https://arxiv.org/pdf/1312.6114.pdf)是該領域的開創性論文。 他們會經歷完整的架構思維過程以及優雅的數學運算。 對于對 VAE 感興趣的任何人，必須閱讀。 另一個有趣的讀物是 Carl Doersch 的論文，[變分編碼器教程](https://arxiv.org/pdf/1606.05908.pdf)。 [Github 鏈接包含 VAE 的另一種實現，以及來自 Kingma 和 Welling 論文的圖像再現](https://github.com/hwalsuklee/tensorflow-mnist-VAE)。 # 通過膠囊網絡學習擊敗 MNIST 的最新結果 膠囊網絡（或 CapsNets）是一種非常新穎的深度學習網絡。 這項技術是在 2017 年 10 月底由 Sara Sabour，Nicholas Frost 和 Geoffrey Hinton 發表的[名為《膠囊之間的動態路由》的開創性論文](https://arxiv.org/abs/1710.09829)中引入的。 欣頓（Hinton）是深度學習之父之一，因此，整個深度學習社區很高興看到膠囊技術取得的進步。 確實，CapsNets 已經在 MNIST 分類中擊敗了最好的 CNN，這真是……令人印象深刻！ **那么 CNN 有什么問題？** 在 CNN 中，每一層*都會以漸進的粒度理解*圖像。 正如我們在多種秘籍中討論的那樣，第一層將最有可能識別直線或簡單的曲線和邊緣，而隨后的層將開始理解更復雜的形狀（例如矩形）和復雜的形式（例如人臉）。 現在，用于 CNN 的一項關鍵操作是池化。 池化旨在創建位置不變性，通常在每個 CNN 層之后使用它來使任何問題在計算上易于處理。 但是，合并會帶來一個嚴重的問題，因為它迫使我們丟失所有位置數據。 不是很好。 考慮一下臉：它由兩只眼睛，一張嘴和一只鼻子組成，重要的是這些部分之間存在空間關系（嘴在鼻子下方，通常在眼睛下方）。 確實，欣頓說： 卷積神經網絡中使用的池化操作是一個很大的錯誤，它運行良好的事實是一場災難。 從技術上講，我們不需要位置不變。 相反，我們需要等方差。 等方差是一個奇特的術語，表示我們想了解圖像中的旋轉或比例變化，并且我們要相應地調整網絡。 這樣，圖像中不同成分的空間定位不會丟失。 **那么膠囊網絡有什么新功能？** 據作者說，我們的大腦有稱為**膠囊**的模塊，每個膠囊專門處理特定類型的信息。 尤其是，有些膠囊對于理解位置的概念，尺寸的概念，方向的概念，變形的概念，紋理等非常有用。 除此之外，這組作者還建議我們的大腦具有特別有效的機制，可以將每條信息動態路由到膠囊，這被認為最適合處理特定類型的信息。 因此，CNN 和 CapsNets 之間的主要區別在于，使用 CNN 時，您會不斷添加用于創建深度網絡的層，而使用 CapsNet 時，您會在另一個內部嵌套神經層。 膠囊是一組神經元，可在網絡中引入更多結構。 它產生一個向量來表示圖像中實體的存在。 尤其是，欣頓使用活動向量的長度來表示實體存在的概率，并使用其方向來表示實例化參數。 當多個預測結果一致時，更高級別的膠囊就會生效。 對于每個可能的父項，膠囊產生一個額外的預測向量。 現在有了第二項創新：我們將使用跨膠囊的動態路由，并且不再使用池化的原始思想。 較低級別的容器傾向于將其輸出發送到較高級別的容器，并且活動向量的標量積很大，而預測來自較低級別的容器。 標量預測向量乘積最大的親本會增加膠囊鍵。 所有其他父項都減少了聯系。 換句話說，這種想法是，如果較高級別的膠囊同意較低級別的膠囊，則它將要求發送更多該類型的信息。 如果沒有協議，它將要求發送更少的協議。 使用協定方法的這種動態路由優于當前的機制（例如最大池），并且根據 Hinton 的說法，路由最終是解析圖像的一種方法。 實際上，最大池化忽略了除最大值以外的任何東西，而動態路由根據較低層和較高層之間的協議選擇性地傳播信息。 第三個差異是引入了新的非線性激活函數。 CapsNet 并未像在 CNN 中那樣向每個層添加擠壓函數，而是向嵌套的一組層添加了擠壓函數。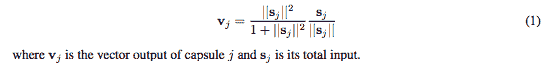 下圖表示了非線性激活函數，它被稱為擠壓函數（方程式 1）：  如欣頓的開創性論文中所示的壓縮函數 此外，Hinton 等人表明，經過判別訓練的多層膠囊系統在 MNIST 上達到了最先進的表現，并且在識別高度重疊的數字方面比卷積網絡要好得多。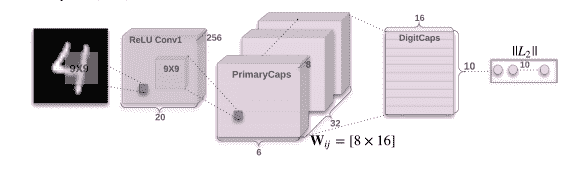 論文《膠囊之間的動態路由》向我們展示了簡單的 CapsNet 架構：  簡單的 CapsNet 架構 該架構很淺，只有兩個卷積層和一個完全連接的層。 Conv1 具有 256 個`9×9`卷積核，步幅為 1，并具有 ReLU 激活函數。 該層的作用是將像素強度轉換為局部特征檢測器的活動，然后將其用作主膠囊的輸入。 PrimaryCapsules 是具有 32 個通道的卷積膠囊層。 每個主膠囊包含 8 個卷積單元，其內核為`9×9`，步幅為 2。 總計，PrimaryCapsules 具有`[32, 6, 6]`膠囊輸出（每個輸出是 8D 向量），并且`[6, 6]`網格中的每個膠囊彼此共享權重。 最后一層（DigitCaps）每位數字類具有一個 16D 膠囊，這些膠囊中的每個膠囊都接收來自下一層中所有其他膠囊的輸入。 路由僅發生在兩個連續的膠囊層之間（例如 PrimaryCapsules 和 DigitCaps）。 # 準備 此秘籍基于[這個頁面](https://github.com/debarko/CapsNet-Tensorflow)上提供的代碼，而該代碼又基于[這個頁面](https://github.com/naturomics/CapsNet-Tensorflow.git)。 # 操作步驟 這是我們如何進行秘籍的方法： 1. 在 Apache Licence 下從 github 克隆代碼： ```py git clone https://github.com/naturomics/CapsNet-Tensorflow.git $ cd CapsNet-Tensorflow ``` 2. 下載 MNIST 并創建適當的結構： ```py mkdir -p data/mnist wget -c -P data/mnist \\ http://yann.lecun.com/exdb/mnist/{train-images-idx3-ubyte.gz,train-labels-idx1-ubyte.gz,t10k-images-idx3-ubyte.gz,t10k-labels-idx1-ubyte.gz} gunzip data/mnist/*.gz ``` 3. 開始訓練過程： ```py python main.py ``` 4. 讓我們看看用于定義膠囊的代碼。 每個膠囊將 4D 張量作為輸入并返回 4D 張量。 可以將膠囊定義為完全連接的網絡（DigiCaps）或卷積網絡（主膠囊）。 請注意，Primary 是卷積網絡的集合，在它們之后應用了非線性壓縮函數。 主膠囊將通過動態路由與 DigiCaps 通信： ```py # capsLayer.py # import numpy as np import tensorflow as tf from config import cfg epsilon = 1e-9 class CapsLayer(object): ''' Capsule layer. Args: input: A 4-D tensor. num_outputs: the number of capsule in this layer. vec_len: integer, the length of the output vector of a capsule. layer_type: string, one of 'FC' or "CONV", the type of this layer, fully connected or convolution, for the future expansion capability with_routing: boolean, this capsule is routing with the lower-level layer capsule. Returns: A 4-D tensor. ''' def __init__(self, num_outputs, vec_len, with_routing=True, layer_type='FC'): self.num_outputs = num_outputs self.vec_len = vec_len self.with_routing = with_routing self.layer_type = layer_type def __call__(self, input, kernel_size=None, stride=None): ''' The parameters 'kernel_size' and 'stride' will be used while 'layer_type' equal 'CONV' ''' if self.layer_type == 'CONV': self.kernel_size = kernel_size self.stride = stride if not self.with_routing: # the PrimaryCaps layer, a convolutional layer # input: [batch_size, 20, 20, 256] assert input.get_shape() == [cfg.batch_size, 20, 20, 256] capsules = [] for i in range(self.vec_len): # each capsule i: [batch_size, 6, 6, 32] with tf.variable_scope('ConvUnit_' + str(i)): caps_i = tf.contrib.layers.conv2d(input, self.num_outputs, self.kernel_size, self.stride, padding="VALID") caps_i = tf.reshape(caps_i, shape=(cfg.batch_size, -1, 1, 1)) capsules.append(caps_i) assert capsules[0].get_shape() == [cfg.batch_size, 1152, 1, 1] # [batch_size, 1152, 8, 1] capsules = tf.concat(capsules, axis=2) capsules = squash(capsules) assert capsules.get_shape() == [cfg.batch_size, 1152, 8, 1] return(capsules) if self.layer_type == 'FC': if self.with_routing: # the DigitCaps layer, a fully connected layer # Reshape the input into [batch_size, 1152, 1, 8, 1] self.input = tf.reshape(input, shape=(cfg.batch_size, -1, 1, input.shape[-2].value, 1)) with tf.variable_scope('routing'): # b_IJ: [1, num_caps_l, num_caps_l_plus_1, 1, 1] b_IJ = tf.constant(np.zeros([1, input.shape[1].value, self.num_outputs, 1, 1], dtype=np.float32)) capsules = routing(self.input, b_IJ) capsules = tf.squeeze(capsules, axis=1) return(capsules) ``` 5. 論文《膠囊之間的動態路由》介紹了路由算法，相關章節中定義了等式 2 和等式 3。該路由算法的目標是將信息從較低層的膠囊傳遞到較高層的膠囊，并且*了解*哪里有一致性。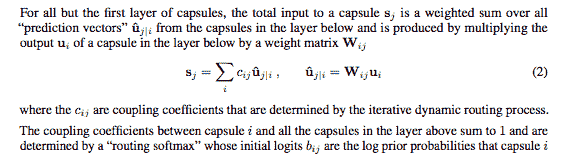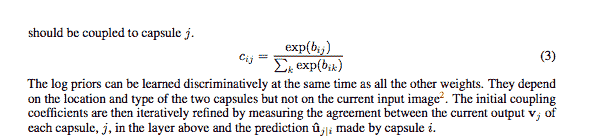 通過簡單地使用上層中每個膠囊`j`的當前輸出`v[j]`，和膠囊`i`得出的預測`u_hat[j|i]`的標量乘積，即可計算出一致性：    以下方法實現了前面圖像中過程 1 中描述的步驟。 注意，輸入是來自`l`層中 1,152 個膠囊的 4D 張量。 輸出是形狀為`[batch_size, 1, length(v_j)=16, 1]`的張量，表示層`l + 1`中膠囊`j`的向量輸出`v[j]`： ```py def routing(input, b_IJ): ''' The routing algorithm. Args: input: A Tensor with [batch_size, num_caps_l=1152, 1, length(u_i)=8, 1] shape, num_caps_l meaning the number of capsule in the layer l. Returns: A Tensor of shape [batch_size, num_caps_l_plus_1, length(v_j)=16, 1] representing the vector output `v_j` in the layer l+1 Notes: u_i represents the vector output of capsule i in the layer l, and v_j the vector output of capsule j in the layer l+1. ''' # W: [num_caps_j, num_caps_i, len_u_i, len_v_j] W = tf.get_variable('Weight', shape=(1, 1152, 10, 8, 16), dtype=tf.float32, initializer=tf.random_normal_initializer(stddev=cfg.stddev)) # Eq.2, calc u_hat # do tiling for input and W before matmul # input => [batch_size, 1152, 10, 8, 1] # W => [batch_size, 1152, 10, 8, 16] input = tf.tile(input, [1, 1, 10, 1, 1]) W = tf.tile(W, [cfg.batch_size, 1, 1, 1, 1]) assert input.get_shape() == [cfg.batch_size, 1152, 10, 8, 1] # in last 2 dims: # [8, 16].T x [8, 1] => [16, 1] => [batch_size, 1152, 10, 16, 1] u_hat = tf.matmul(W, input, transpose_a=True) assert u_hat.get_shape() == [cfg.batch_size, 1152, 10, 16, 1] # line 3,for r iterations do for r_iter in range(cfg.iter_routing): with tf.variable_scope('iter_' + str(r_iter)): # line 4: # => [1, 1152, 10, 1, 1] c_IJ = tf.nn.softmax(b_IJ, dim=2) c_IJ = tf.tile(c_IJ, [cfg.batch_size, 1, 1, 1, 1]) assert c_IJ.get_shape() == [cfg.batch_size, 1152, 10, 1, 1] # line 5: # weighting u_hat with c_IJ, element-wise in the last two dims # => [batch_size, 1152, 10, 16, 1] s_J = tf.multiply(c_IJ, u_hat) # then sum in the second dim, resulting in [batch_size, 1, 10, 16, 1] s_J = tf.reduce_sum(s_J, axis=1, keep_dims=True) assert s_J.get_shape() == [cfg.batch_size, 1, 10, 16, 16 # line 6: # squash using Eq.1, v_J = squash(s_J) assert v_J.get_shape() == [cfg.batch_size, 1, 10, 16, 1] # line 7: # reshape & tile v_j from [batch_size ,1, 10, 16, 1] to [batch_size, 10, 1152, 16, 1] # then matmul in the last tow dim: [16, 1].T x [16, 1] => [1, 1], reduce mean in the # batch_size dim, resulting in [1, 1152, 10, 1, 1] v_J_tiled = tf.tile(v_J, [1, 1152, 1, 1, 1]) u_produce_v = tf.matmul(u_hat, v_J_tiled, transpose_a=True) assert u_produce_v.get_shape() == [cfg.batch_size, 1152, 10, 1, 1] b_IJ += tf.reduce_sum(u_produce_v, axis=0, keep_dims=True) return(v_J) ``` 6. 現在讓我們回顧一下非線性激活壓縮函數。 輸入是具有`[batch_size, num_caps, vec_len, 1]`形狀的 4D 向量，輸出是具有與向量相同形狀但被壓縮在第三維和第四維中的 4-D 張量。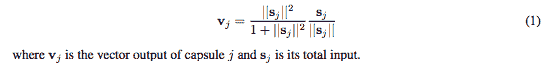 給定一個向量輸入，目標是計算公式 1 中表示的值，如下所示：  ```py def squash(vector): '''Squashing function corresponding to Eq. 1 Args: vector: A 5-D tensor with shape [batch_size, 1, num_caps, vec_len, 1], Returns: A 5-D tensor with the same shape as vector but squashed in 4rd and 5th dimensions. ''' vec_squared_norm = tf.reduce_sum(tf.square(vector), -2, keep_dims=True) scalar_factor = vec_squared_norm / (1 + vec_squared_norm) / tf.sqrt(vec_squared_norm + epsilon) vec_squashed = scalar_factor * vector # element-wise return(vec_squashed) ``` 7. 在前面的步驟中，我們定義了什么是膠囊，膠囊之間的動態路由算法，以及非線性壓縮函數。 現在我們可以定義適當的 CapsNet。 構建損失函數以進行訓練，并選擇了 Adam 優化器。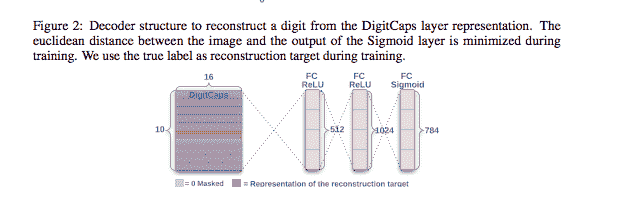 方法`build_arch(...)`定義了 CapsNet，如下圖所示：  請注意，本文將重構技術描述為一種正則化方法。 從本文： 我們使用額外的重建損失來鼓勵數字囊對輸入數字的實例化參數進行編碼。 在訓練過程中，我們會掩蓋除正確數字膠囊外的所有活動向量。 然后，我們使用此活動向量進行重構。 數字膠囊的輸出被饋送到解碼器，該解碼器由三個完全連接的層組成，這些層對像素強度進行建模，如圖 2 所示。我們將邏輯單元的輸出與像素強度之間的平方差之和最小化。 我們將這種重建損失降低了 0.0005，以使其在訓練過程中不會控制保證金損失。 如下實現的方法`build_arch(..)`也用于創建解碼器：  ```py #capsNet.py # import tensorflow as tf from config import cfg from utils import get_batch_data from capsLayer import CapsLayer epsilon = 1e-9 class CapsNet(object): def __init__(self, is_training=True): self.graph = tf.Graph() with self.graph.as_default(): if is_training: self.X, self.labels = get_batch_data() self.Y = tf.one_hot(self.labels, depth=10, axis=1, dtype=tf.float32) self.build_arch() self.loss() self._summary() # t_vars = tf.trainable_variables() self.global_step = tf.Variable(0, name='global_step', trainable=False) self.optimizer = tf.train.AdamOptimizer() self.train_op = self.optimizer.minimize(self.total_loss, global_step=self.global_step) # var_list=t_vars) elif cfg.mask_with_y: self.X = tf.placeholder(tf.float32, shape=(cfg.batch_size, 28, 28, 1)) self.Y = tf.placeholder(tf.float32, shape=(cfg.batch_size, 10, 1)) self.build_arch() else: self.X = tf.placeholder(tf.float32, shape=(cfg.batch_size, 28, 28, 1)) self.build_arch() tf.logging.info('Setting up the main structure') def build_arch(self): with tf.variable_scope('Conv1_layer'): # Conv1, [batch_size, 20, 20, 256] conv1 = tf.contrib.layers.conv2d(self.X, num_outputs=256, kernel_size=9, stride=1, padding='VALID') assert conv1.get_shape() == [cfg.batch_size, 20, 20, 256]# Primary Capsules layer, return [batch_size, 1152, 8, 1] with tf.variable_scope('PrimaryCaps_layer'): primaryCaps = CapsLayer(num_outputs=32, vec_len=8, with_routing=False, layer_type='CONV') caps1 = primaryCaps(conv1, kernel_size=9, stride=2) assert caps1.get_shape() == [cfg.batch_size, 1152, 8, 1] # DigitCaps layer, return [batch_size, 10, 16, 1] with tf.variable_scope('DigitCaps_layer'): digitCaps = CapsLayer(num_outputs=10, vec_len=16, with_routing=True, layer_type='FC') self.caps2 = digitCaps(caps1) # Decoder structure in Fig. 2 # 1\. Do masking, how: with tf.variable_scope('Masking'): # a). calc ||v_c||, then do softmax(||v_c||) # [batch_size, 10, 16, 1] => [batch_size, 10, 1, 1] self.v_length = tf.sqrt(tf.reduce_sum(tf.square(self.caps2), axis=2, keep_dims=True) + epsilon) self.softmax_v = tf.nn.softmax(self.v_length, dim=1) assert self.softmax_v.get_shape() == [cfg.batch_size, 10, 1, 1] # b). pick out the index of max softmax val of the 10 caps # [batch_size, 10, 1, 1] => [batch_size] (index) self.argmax_idx = tf.to_int32(tf.argmax(self.softmax_v, axis=1)) assert self.argmax_idx.get_shape() == [cfg.batch_size, 1, 1] self.argmax_idx = tf.reshape(self.argmax_idx, shape=(cfg.batch_size, )) . # Method 1. if not cfg.mask_with_y: # c). indexing # It's not easy to understand the indexing process with argmax_idx # as we are 3-dim animal masked_v = [] for batch_size in range(cfg.batch_size): v = self.caps2[batch_size][self.argmax_idx[batch_size], :] masked_v.append(tf.reshape(v, shape=(1, 1, 16, 1))) self.masked_v = tf.concat(masked_v, axis=0) assert self.masked_v.get_shape() == [cfg.batch_size, 1, 16, 1] # Method 2\. masking with true label, default mode else: self.masked_v = tf.matmul(tf.squeeze(self.caps2), tf.reshape(self.Y, (-1, 10, 1)), transpose_a=True) self.v_length = tf.sqrt(tf.reduce_sum(tf.square(self.caps2), axis=2, keep_dims=True) + epsilon) # 2\. Reconstruct the MNIST images with 3 FC layers # [batch_size, 1, 16, 1] => [batch_size, 16] => [batch_size, 512] with tf.variable_scope('Decoder'): vector_j = tf.reshape(self.masked_v, shape=(cfg.batch_size, -1)) fc1 = tf.contrib.layers.fully_connected(vector_j, num_outputs=512) assert fc1.get_shape() == [cfg.batch_size, 512] fc2 = tf.contrib.layers.fully_connected(fc1, num_outputs=1024) assert fc2.get_shape() == [cfg.batch_size, 1024] self.decoded = tf.contrib.layers.fully_connected(fc2, num_outputs=784, activation_fn=tf.sigmoid) ``` 8. 本文中定義的另一個重要部分是保證金損失函數。 這在下面的論文（等式 4）的摘錄引用中進行了說明，并在`loss(..)`方法中實現，該方法包括三個損失，即邊際損失，重建損失和總損失：  ```py def loss(self): # 1\. The margin loss # [batch_size, 10, 1, 1] # max_l = max(0, m_plus-||v_c||)^2 max_l = tf.square(tf.maximum(0., cfg.m_plus - self.v_length)) # max_r = max(0, ||v_c||-m_minus)^2 max_r = tf.square(tf.maximum(0., self.v_length - cfg.m_minus)) assert max_l.get_shape() == [cfg.batch_size, 10, 1, 1] # reshape: [batch_size, 10, 1, 1] => [batch_size, 10] max_l = tf.reshape(max_l, shape=(cfg.batch_size, -1)) max_r = tf.reshape(max_r, shape=(cfg.batch_size, -1)) # calc T_c: [batch_size, 10] T_c = self.Y # [batch_size, 10], element-wise multiply L_c = T_c * max_l + cfg.lambda_val * (1 - T_c) * max_r self.margin_loss = tf.reduce_mean(tf.reduce_sum(L_c, axis=1)) # 2\. The reconstruction loss orgin = tf.reshape(self.X, shape=(cfg.batch_size, -1)) squared = tf.square(self.decoded - orgin) self.reconstruction_err = tf.reduce_mean(squared) # 3\. Total loss # The paper uses sum of squared error as reconstruction error, but we # have used reduce_mean in `# 2 The reconstruction loss` to calculate # mean squared error. In order to keep in line with the paper,the # regularization scale should be 0.0005*784=0.392 self.total_loss = self.margin_loss + cfg.regularization_scale * self.reconstruction_err ``` 9. 另外，定義`a _summary(...)`方法來報告損失和準確率可能會很方便： ```py #Summary def _summary(self): train_summary = [] train_summary.append(tf.summary.scalar('train/margin_loss', self.margin_loss))train_summary.append(tf.summary.scalar('train/reconstruction_loss', self.reconstruction_err)) train_summary.append(tf.summary.scalar('train/total_loss', self.total_loss)) recon_img = tf.reshape(self.decoded, shape=(cfg.batch_size, 28, 28, 1)) train_summary.append(tf.summary.image('reconstruction_img', recon_img)) correct_prediction = tf.equal(tf.to_int32(self.labels), self.argmax_idx) self.batch_accuracy = tf.reduce_sum(tf.cast(correct_prediction, tf.float32)) self.test_acc = tf.placeholder_with_default(tf.constant(0.), shape=[]) test_summary = [] test_summary.append(tf.summary.scalar('test/accuracy', self.test_acc)) self.train_summary = tf.summary.merge(train_summary) self.test_summary = tf.summary.merge(test_summary) ``` # 工作原理 CapsNet 與最先進的深度學習網絡有很大的不同。 CapsNet 并沒有添加更多的層并使網絡更深，而是使用了淺層網絡，其中，膠囊層嵌套在其他層內。 每個膠囊專門用于檢測圖像中的特定實體，并且使用動態路由機制將檢測到的實體發送給父層。 使用 CNN，您必須從許多不同角度考慮成千上萬張圖像，以便從不同角度識別物體。 Hinton 認為，這些層中的冗余將使膠囊網絡能夠從多個角度和在不同情況下以 CNN 通常使用的較少數據識別對象。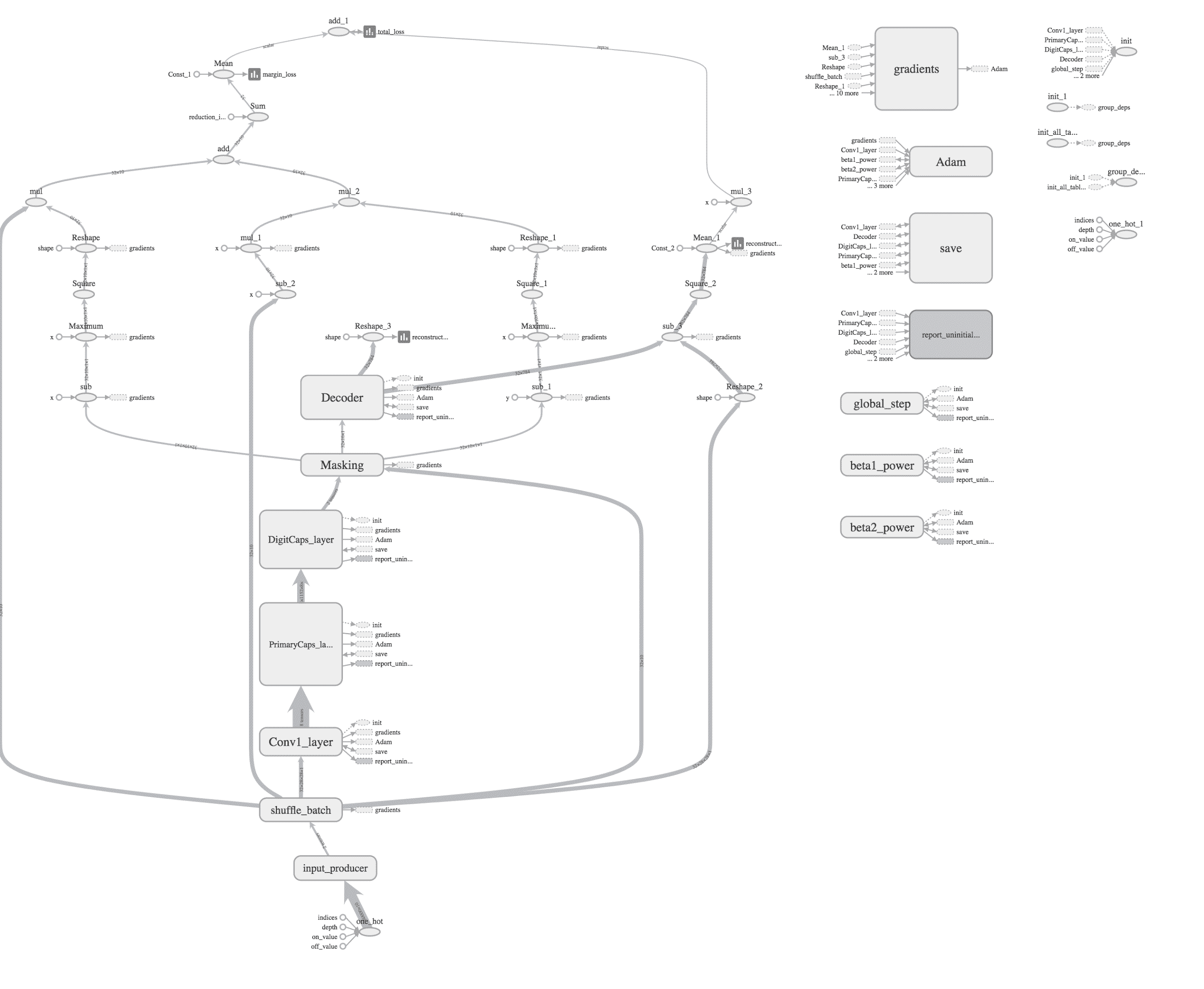 讓我們檢查一下 tensorboad 所示的網絡：  代碼中定義并由 tensorboard 顯示的 CapsNet 示例 如下圖所示，其結果令人印象深刻。 CapsNet 在以前僅在更深層的網絡中才能實現的三層網絡上具有較低的測試誤差（0.25%）。 基線是具有`256, 256-128`個通道的三個卷積層的標準 CNN。 每個都有`5 x 5`個內核，步幅為 1。最后一個卷積層后面是兩個大小為`328, 192` 的完全連接的層。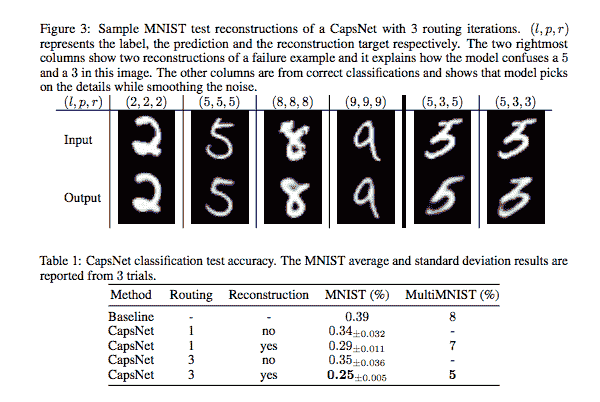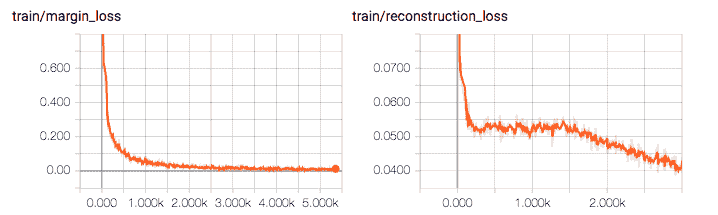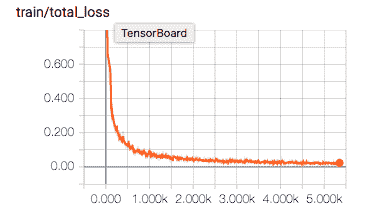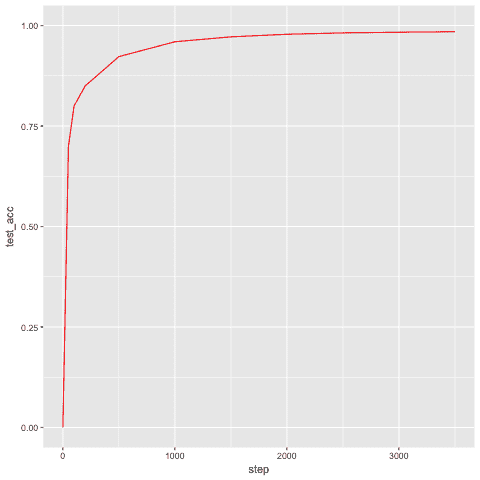 最后一個完全連接的層通過壓降連接到具有交叉熵損失的 10 類 softmax 層：  讓我們檢查保證金損失，重建損失和總損失的減少：   我們還要檢查準確率的提高； 經過 500 次迭代，它在 3500 次迭代中分別達到 92% 和 98.46% ：  | **迭代** | **精度** | | --- | --- | | 500 | 0.922776442308 | | 1000 | 0.959735576923 | | 1500 | 0.971955128205 | | 2000 | 0.978365384615 | | 2500 | 0.981770833333 | | 3000 | 0.983473557692 | | 3500 | 0.984675480769 | CapsNet 提高準確率的示例 # 更多 CapsNets 在 MNIST 上可以很好地工作，但是在理解是否可以在其他數據集（例如 CIFAR）或更通用的圖像集合上獲得相同的令人印象深刻的結果方面，還有很多研究工作要做。 如果您有興趣了解更多信息，請查看以下內容： [Google 的 AI 向導在神經網絡上帶來了新的變化](https://www.wired.com/story/googles-ai-wizard-unveils-a-new-twist-on-neural-networks/) [Google 研究人員可以替代傳統神經網絡](https://www.technologyreview.com/the-download/609297/google-researchers-have-a-new-alternative-to-traditional-neural-networks/) Keras-CapsNet 是可在[這個頁面](https://github.com/XifengGuo/CapsNet-Keras)上使用的 Keras 實現。 [杰弗里·欣頓（Geoffrey Hinton）討論了卷積神經網絡的問題](https://www.youtube.com/watch?v=rTawFwUvnLE&feature=youtu.be)