# 五、使用 TensorFlow 實現自編碼器 訓練自編碼器是一個簡單的過程。它是一個 NN，其輸出與其輸入相同。有一個輸入層，后面是幾個隱藏層，然后在一定深度之后，隱藏層遵循反向架構，直到我們到達最終層與輸入層相同的點。我們將數據傳遞到我們希望學習嵌入的網絡中。 在此示例中，我們使用來自 MNIST 數據集的圖像作為輸入。我們通過導入所有主庫來開始實現： ```py import tensorflow as tf import numpy as np import matplotlib.pyplot as plt ``` 然后我們準備 MNIST 數據集。我們使用 TensorFlow 中的內置`input_data`類來加載和設置數據。此類確保下載和預處理數據以供自編碼器使用。因此，基本上，我們根本不需要進行任何特征工程： ```py from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("MNIST_data/",one_hot=True) ``` 在前面的代碼塊中，`one_hot=True`參數確保所有特征都是熱編碼的。單熱編碼是一種技術，通過該技術將分類變量轉換為可以饋入 ML 算法的形式。 接下來，我們配置網絡參數： ```py learning_rate = 0.01 training_epochs = 20 batch_size = 256 display_step = 1 examples_to_show = 20 ``` 輸入圖像的大小如下： ```py n_input = 784 ``` 隱藏層的大小如下： ```py n_hidden_1 = 256 n_hidden_2 = 128 ``` 最終尺寸對應于`28×28 = 784`像素。 我們需要為輸入圖像定義占位符變量。該張量的數據類型設置為`float`，因為`mnist`值的比例為[0,1]，形狀設置為`[None, n_input]`。定義`None`參數意味著張量可以包含任意數量的圖像： ```py X = tf.placeholder("float", [None, n_input]) ``` 然后我們可以定義網絡的權重和偏置。`weights`數據結構包含編碼器和解碼器的權重定義。請注意，使用`tf.random_normal`選擇權重，它返回具有正態分布的隨機值： ```py weights = { 'encoder_h1': tf.Variable\ (tf.random_normal([n_input, n_hidden_1])), 'encoder_h2': tf.Variable\ (tf.random_normal([n_hidden_1, n_hidden_2])), 'decoder_h1': tf.Variable\ (tf.random_normal([n_hidden_2, n_hidden_1])), 'decoder_h2': tf.Variable\ (tf.random_normal([n_hidden_1, n_input])), } ``` 同樣，我們定義了網絡的偏置： ```py biases = { 'encoder_b1': tf.Variable\ (tf.random_normal([n_hidden_1])), 'encoder_b2': tf.Variable\ (tf.random_normal([n_hidden_2])), 'decoder_b1': tf.Variable\ (tf.random_normal([n_hidden_1])), 'decoder_b2': tf.Variable\ (tf.random_normal([n_input])), } ``` 我們將網絡建模分為兩個互補的完全連接的網絡：編碼器和解碼器。編碼器對數據進行編碼；它從 MNIST 數據集中輸入圖像`X`，并執行數據編碼： ```py encoder_in = tf.nn.sigmoid(tf.add\ (tf.matmul(X, \ weights['encoder_h1']),\ biases['encoder_b1'])) ``` 輸入數據編碼只是矩陣乘法運算。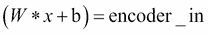使用矩陣乘法將維度 784 的輸入數據`X`減少到較低維度 256：  這里，`W`是權重張量，`encoder_h1`，`b`是偏置張量，`encoder_b1`。通過這個操作，我們將初始圖像編碼為自編碼器的有用輸入。編碼過程的第二步包括數據壓縮。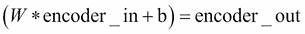輸入`encoder_in`張量表示的數據通過第二個矩陣乘法運算減小到較小的大小： ```py encoder_out = tf.nn.sigmoid(tf.add\ (tf.matmul(encoder_in,\ weights['encoder_h2']),\ biases['encoder_b2'])) ``` 然后將尺寸 256 的輸入數據`encoder_in`壓縮到 128 的較小張量：  這里，`W`代表權重張量`encoder_h2`，而`b`代表偏差張量，`encoder_b2`。請注意，我們使用 sigmoid 作為編碼器階段的激活函數。 解碼器執行編碼器的逆操作。它解壓縮輸入以獲得相同大小的網絡輸入的輸出。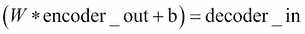該過程的第一步是將大小為 128 的`encoder_out`張量轉換為 256 大小的中間表示的張量： ```py decoder_in = tf.nn.sigmoid(tf.add\ (tf.matmul(encoder_out,\ weights['decoder_h1']),\ biases['decoder_b1'])) ``` 在公式中，它意味著：  這里，`W`是權重張量，`decoder_h1`，大小`256×128`，`b`是偏置張量，`decoder_b1`，大小 256。最終解碼操作是將數據從其中間表示（大小為 256）解壓縮到最終表示（維度 784），這是原始數據的大小： ```py decoder_out = tf.nn.sigmoid(tf.add\ (tf.matmul(decoder_in,\ weights['decoder_h2']),\ biases['decoder_b2'])) ``` `y_pred`參數設置為`decoder_out`： ```py y_pred = decoder_out ``` 網絡將了解輸入數據`X`是否等于解碼數據，因此我們定義以下內容： ```py y_true = X ``` 自編碼器的要點是創建一個擅長重建原始數據的縮減矩陣。因此，我們希望最小化`cost`函數。然后我們將`cost`函數定義為`y_true`和`y_pred`之間的均方誤差： ```py cost = tf.reduce_mean(tf.pow(y_true - y_pred, 2)) ``` 為了優化`cost`函數，我們使用以下`RMSPropOptimizer`類： ```py optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(cost) ``` 然后我們準備啟動會話： ```py init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) ``` 我們需要設置批量圖像的大小來訓練網絡： ```py total_batch = int(mnist.train.num_examples/batch_size) ``` 從訓練周期開始（`training_epochs`的數量設置為`10`）： ```py for epoch in range(training_epochs): ``` 循環遍歷所有批次： ```py for i in range(total_batch): batch_xs, batch_ys =\ mnist.train.next_batch(batch_size) ``` 然后我們運行優化程序，用批量集`batch_xs`提供執行圖： ```py _, c = sess.run([optimizer, cost],\ feed_dict={X: batch_xs}) ``` 接下來，我們顯示每個`epoch`步驟的結果： ```py if epoch % display_step == 0: print(?Epoch:", ?%04d' % (epoch+1), ?cost=", ?{:.9f}".format(c)) print("Optimization Finished!") ``` 最后，我們使用編碼或解碼程序測試模型 。我們為模型提供圖像子集，其中`example_to_show`的值設置為`4`： ```py encode_decode = sess.run( y_pred, feed_dict=\ {X: mnist.test.images[:examples_to_show]}) ``` 我們使用 Matplotlib 比較原始圖像和它們的重建： ```py f, a = plt.subplots(2, 10, figsize=(10, 2)) for i in range(examples_to_show): a[0][i].imshow(np.reshape(mnist.test.images[i], (28, 28))) a[1][i].imshow(np.reshape(encode_decode[i], (28, 28))) f.show() plt.draw() plt.show() ``` 當我們運行會話時，我們應該有這樣的輸出： ```py Extracting MNIST_data/train-images-idx3-ubyte.gz Extracting MNIST_data/train-labels-idx1-ubyte.gz Extracting MNIST_data/t10k-images-idx3-ubyte.gz Extracting MNIST_data/t10k-labels-idx1-ubyte.gz Epoch: 0001 cost= 0.208461761 Epoch: 0002 cost= 0.172908291 Epoch: 0003 cost= 0.153524384 Epoch: 0004 cost= 0.144243762 Epoch: 0005 cost= 0.137013704 Epoch: 0006 cost= 0.127291277 Epoch: 0007 cost= 0.125370100 Epoch: 0008 cost= 0.121299766 Epoch: 0009 cost= 0.111687921 Epoch: 0010 cost= 0.108801551 Epoch: 0011 cost= 0.105516203 Epoch: 0012 cost= 0.104304880 Epoch: 0013 cost= 0.103362709 Epoch: 0014 cost= 0.101118311 Epoch: 0015 cost= 0.098779991 Epoch: 0016 cost= 0.095374011 Epoch: 0017 cost= 0.095469855 Epoch: 0018 cost= 0.094381645 Epoch: 0019 cost= 0.090281256 Epoch: 0020 cost= 0.092290156 Optimization Finished! ``` 然后我們顯示結果。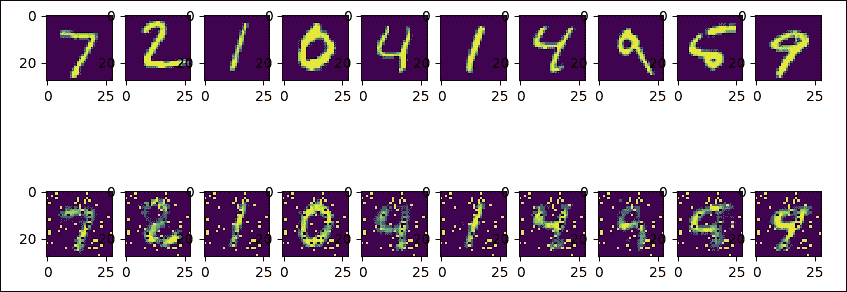第一行是原始圖像，第二行是解碼圖像：  圖 4：原始和解碼的 MNIST 圖像 如你所見，第二個與原來的不同（它似乎仍然是數字二，就像三個一樣）。我們可以增加周期數或更改網絡參數以改善結果。 # 提高自編碼器的魯棒性 我們可以用來改善模型穩健性的成功策略，是在編碼階段引入噪聲。我們將去噪自編碼器稱為自編碼器的隨機版本；在去噪自編碼器中，輸入被隨機破壞，但相同輸入的未破壞版本被用作解碼階段的目標。 直覺上， 去噪自編碼器做了兩件事：首先，它試圖對輸入進行編碼，保留相關信息；然后，它試圖消除應用于同一輸入的腐敗過程的影響。在下一節中，我們將展示一個去噪自編碼器的實現。 ## 實現去噪自編碼器 網絡架構非常簡單。 784 像素的輸入圖像被隨機破壞，然后通過編碼網絡層進行尺寸縮減。圖像尺寸從 784 減少到 256 像素。 在解碼階段，我們準備網絡輸出，將圖像大小返回到 784 像素。像往常一樣，我們開始將所有必要的庫加載到我們的實現中： ```py import numpy as np import tensorflow as tf import matplotlib.pyplot as plt from tensorflow.examples.tutorials.mnist import input_data ``` 然后我們設置基本的網絡參數： ```py n_input = 784 n_hidden_1 = 1024 n_hidden_2 = 2048 n_output = 784 ``` 我們設置會話的參數： ```py epochs = 100 batch_size = 100 disp_step = 10 ``` 我們構建訓練和測試集。我們再次使用從`tensorflow.examples.tutorials.mnist`導入的`input_data`函數： ```py print ("PACKAGES LOADED") mnist = input_data.read_data_sets('data/', one_hot=True) trainimg = mnist.train.images trainlabel = mnist.train.labels testimg = mnist.test.images testlabel = mnist.test.labels print ("MNIST LOADED") ``` 讓我們為輸入圖像定義一個占位符變量。數據類型設置為`float`，形狀設置為`[None, n_input]`。`None`參數表示張量可以保持任意數量的圖像，每個圖像的大小為`n_input`： ```py x = tf.placeholder("float", [None, n_input]) ``` 接下來，我們有一個占位符變量，用于與在占位符變量`x`中輸入的圖像相關聯的真實標簽。這個占位符變量的形狀是`[None, n_output]`，這意味著它可以包含任意數量的標簽，并且每個標簽都是長度為`n_output`的向量，在這種情況下為`10`： ```py y = tf.placeholder("float", [None, n_output]) ``` 為了減少過擬合，我們在編碼和解碼過程之前應用一個丟棄，因此我們必須定義一個占位符，以便在丟棄期間保持神經元輸出的概率： ```py dropout_keep_prob = tf.placeholder("float") ``` 在這些定義中，我們修正了權重和網絡偏差： ```py weights = { 'h1': tf.Variable(tf.random_normal([n_input, n_hidden_1])), 'h2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])), 'out': tf.Variable(tf.random_normal([n_hidden_2, n_output])) } biases = { 'b1': tf.Variable(tf.random_normal([n_hidden_1])), 'b2': tf.Variable(tf.random_normal([n_hidden_2])), 'out': tf.Variable(tf.random_normal([n_output])) } ``` 使用`tf.random_normal`選擇`weights`和`biases`值，它返回具有正態分布的隨機值。編碼階段將來自 MNIST 數據集的圖像作為輸入，然后通過應用矩陣乘法運算來執行數據壓縮： ```py encode_in = tf.nn.sigmoid\ (tf.add(tf.matmul\ (x, weights['h1']),\ biases['b1'])) encode_out = tf.nn.dropout\ (encode_in, dropout_keep_prob) ``` 在解碼階段，我們應用相同的過程： ```py decode_in = tf.nn.sigmoid\ (tf.add(tf.matmul\ (encode_out, weights['h2']),\ biases['b2'])) ``` 過擬合的減少是通過丟棄程序來完成的： ```py decode_out = tf.nn.dropout(decode_in,\ dropout_keep_prob) ``` 最后，我們準備構建預測張量，`y_pred`： ```py y_pred = tf.nn.sigmoid\ (tf.matmul(decode_out,\ weights['out']) +\ biases['out']) ``` 然后我們定義一個成本度量， 用于指導變量優化過程： ```py cost = tf.reduce_mean(tf.pow(y_pred - y, 2)) ``` 我們將使用`RMSPropOptimizer`類最小化`cost`函數： ```py optimizer = tf.train.RMSPropOptimizer(0.01).minimize(cost) ``` 最后，我們可以按如下方式初始化已定義的變量： ```py init = tf.global_variables_initializer() ``` 然后我們設置 TensorFlow 的運行會話： ```py with tf.Session() as sess: sess.run(init) print ("Start Training") for epoch in range(epochs): num_batch = int(mnist.train.num_examples/batch_size) total_cost = 0. for i in range(num_batch): ``` 對于每個訓練周期，我們從訓練數據集中選擇一個較小的批次集： ```py batch_xs, batch_ys = \ mnist.train.next_batch(batch_size) ``` 這是焦點。我們使用之前導入的 NumPy 包中的`randn`函數隨機破壞`batch_xs`集： ```py batch_xs_noisy = batch_xs + \ 0.3*np.random.randn(batch_size, 784) ``` 我們使用這些集來提供執行圖，然后運行會話（`sess.run`）： ```py feeds = {x: batch_xs_noisy,\ y: batch_xs, \ dropout_keep_prob: 0.8} sess.run(optimizer, feed_dict=feeds) total_cost += sess.run(cost, feed_dict=feeds) ``` 每十個周期，將顯示平均成本值： ```py if epoch % disp_step == 0: print("Epoch %02d/%02d average cost: %.6f" % (epoch, epochs, total_cost/num_batch)) ``` 最后，我們開始測試訓練有素的模型： ```py print("Start Test") ``` 為此，我們從測試集中隨機選擇一個圖像： ```py randidx = np.random.randint\ (testimg.shape[0], size=1) orgvec = testimg[randidx, :] testvec = testimg[randidx, :] label = np.argmax(testlabel[randidx, :], 1) print("Test label is %d" % (label)) noisyvec = testvec + 0.3*np.random.randn(1, 784) ``` 然后我們在選定的圖像上運行訓練模型： ```py outvec = sess.run(y_pred,\ feed_dict={x: noisyvec,\ dropout_keep_prob: 1}) ``` 正如我們將看到的，以下`plotresult`函數將顯示原始圖像，噪聲圖像和預測圖像： ```py plotresult(orgvec,noisyvec,outvec) print("restart Training") ``` 當我們運行會話時，我們應該看到如下結果： ```py PACKAGES LOADED Extracting data/train-images-idx3-ubyte.gz Extracting data/train-labels-idx1-ubyte.gz Extracting data/t10k-images-idx3-ubyte.gz Extracting data/t10k-labels-idx1-ubyte.gz MNIST LOADED Start Training ``` 為簡潔起見，我們僅報告了 100 個周期后的結果： ```py Epoch 100/100 average cost: 0.212313 Start Test Test label is 6 ``` 這些是原始圖像和噪聲圖像（如您所見，數字 6）：  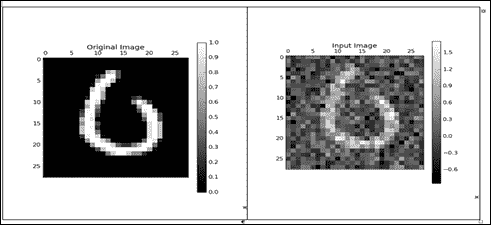圖 5：原始圖像和噪聲圖像 這是一個嚴格重建的圖像：  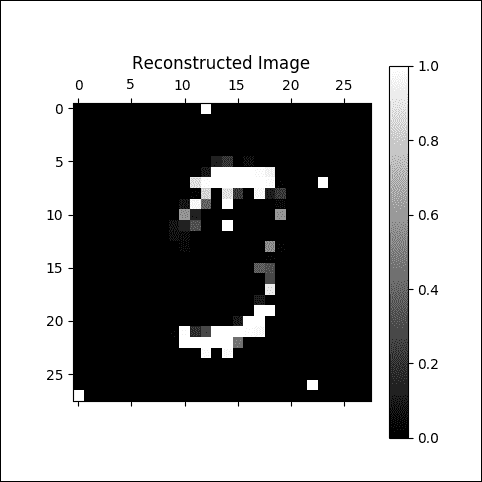圖 6：嚴重重建的圖像 在 100 個周期之后，我們有了更好的結果： ```py Epoch 100/100 average cost: 0.018221 Start Test Test label is 5 ``` 這是原版和噪聲圖像：  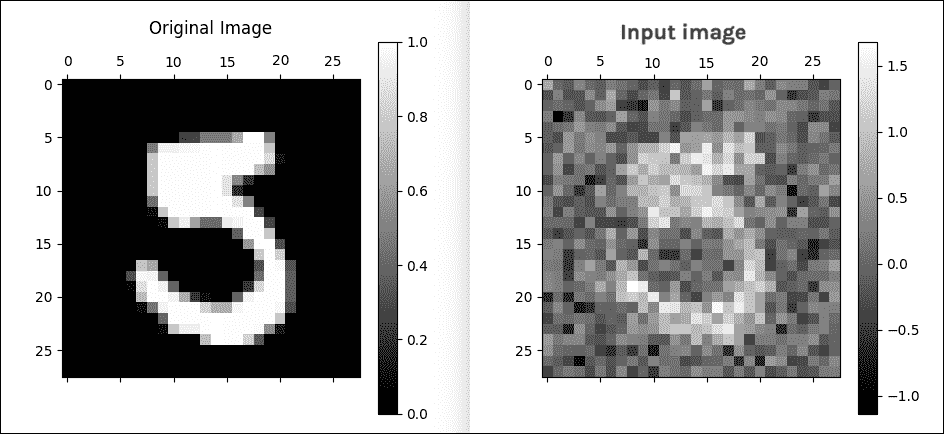圖 7：原始圖像和噪聲圖像 這是一個很好的重建圖像：  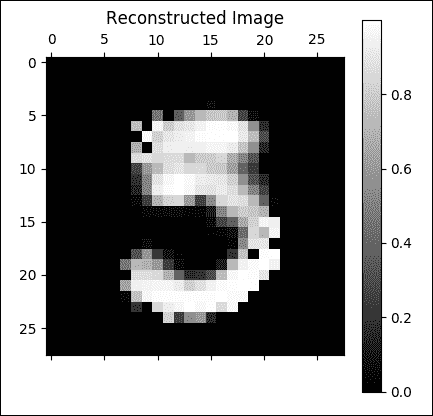圖 8：良好的重建圖像 ## 實現卷積自編碼器 到目前為止，我們已經看到自編碼器輸入是圖像。因此，有必要問一下卷積架構是否可以在我們之前展示的自編碼器架構上更好地工作。我們將分析編碼器和解碼器在卷積自編碼器中的工作原理。 ### 編碼器 編碼器由三個卷積層組成。特征數量從輸入數據 1 變為第一卷積層的 16；然后，第二層從 16 到 32；最后，從最后一個卷積層的 32 到 64。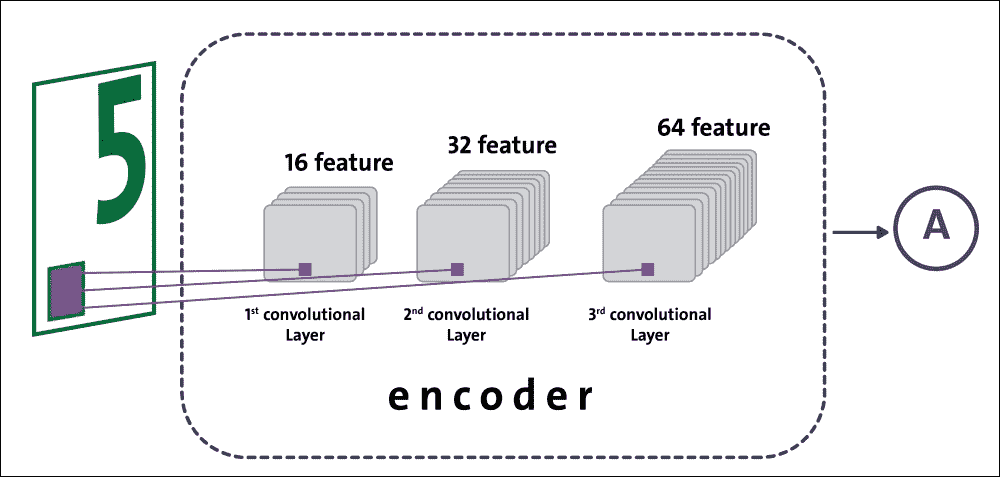從卷積層移動到另一個層時，形狀經歷圖像壓縮：  圖 9：編碼階段的數據流 ### 解碼器 解碼器由三個依次排列的反卷積層組成。對于每個反卷積操作，我們減少特征的數量以獲得必須與原始圖像大小相同的圖像。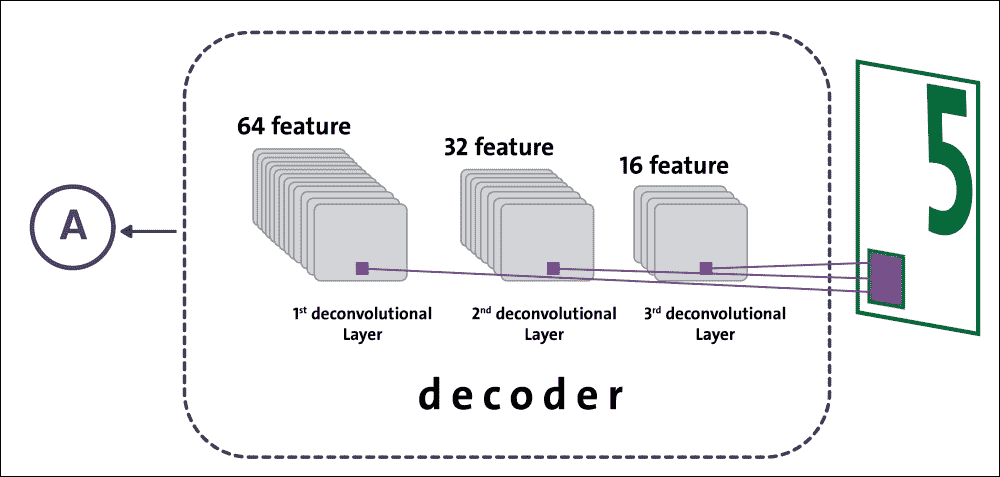除了減少特征數量外，反卷積還可以轉換圖像的形狀：  圖 10：解碼階段的數據流 我們已經準備好了解如何實現卷積自編碼器；第一個實現步驟是加載基本庫： ```py import matplotlib.pyplot as plt import numpy as np import math import tensorflow as tf import tensorflow.examples.tutorials.mnist.input_data as input_data ``` 然后我們構建訓練和測試集： ```py mnist = input_data.read_data_sets("data/", one_hot=True) trainings = mnist.train.images trainlabels = mnist.train.labels testings = mnist.test.images testlabels = mnist.test.labels ntrain = trainings.shape[0] ntest = testings.shape[0] dim = trainings.shape[1] nout = trainlabels.shape[1] ``` 我們需要為輸入圖像定義占位符變量： ```py x = tf.placeholder(tf.float32, [None, dim]) ``` 數據類型設置為`float32`，形狀設置為`[None, dim]`，其中`None`表示張量可以保持任意數量的圖像，每個圖像是長度為`dim`的向量。接下來，我們為輸出圖像提供占位符變量。此變量的形狀設置為`[None, dim]`與輸入形狀相同： ```py y = tf.placeholder(tf.float32, [None, dim]) ``` 然后我們定義`keepprob`變量，[用于配置在網絡訓練期間使用的丟棄率](https://www.tensorflow.org/tutorials/layers#dropout)： ```py keepprob = tf.placeholder(tf.float32) ``` 此外，我們必須定義每個網絡層中的節點數： ```py n1 = 16 n2 = 32 n3 = 64 ksize = 5 ``` 網絡總共包含六層。前三層是卷積的，屬于編碼階段，而后三層是解卷積的，是解碼階段的一部分： ```py weights = { 'ce1': tf.Variable(tf.random_normal\ ([ksize, ksize, 1, n1],stddev=0.1)), 'ce2': tf.Variable(tf.random_normal\ ([ksize, ksize, n1, n2],stddev=0.1)), 'ce3': tf.Variable(tf.random_normal\ ([ksize, ksize, n2, n3],stddev=0.1)), 'cd3': tf.Variable(tf.random_normal\ ([ksize, ksize, n2, n3],stddev=0.1)), 'cd2': tf.Variable(tf.random_normal\ ([ksize, ksize, n1, n2],stddev=0.1)), 'cd1': tf.Variable(tf.random_normal\ ([ksize, ksize, 1, n1],stddev=0.1)) } biases = { 'be1': tf.Variable\ (tf.random_normal([n1], stddev=0.1)), 'be2': tf.Variable\ (tf.random_normal([n2], stddev=0.1)), 'be3': tf.Variable\ (tf.random_normal([n3], stddev=0.1)), 'bd3': tf.Variable\ (tf.random_normal([n2], stddev=0.1)), 'bd2': tf.Variable\ (tf.random_normal([n1], stddev=0.1)), 'bd1': tf.Variable\ (tf.random_normal([1], stddev=0.1)) } ``` 以下函數`cae`構建卷積自編碼器：傳遞的輸入是圖像，`_X`;數據結構權重和偏置，`_W`和`_b`;和`_keepprob`參數： ```py def cae(_X, _W, _b, _keepprob): ``` 最初的 784 像素圖像必須重新整形為`28×28`矩陣，隨后由下一個卷積層處理： ```py _input_r = tf.reshape(_X, shape=[-1, 28, 28, 1]) ``` 第一個卷積層是`_ce1`。相對于輸入圖像，它有`_input_r`張量作為輸入： ```py _ce1 = tf.nn.sigmoid\ (tf.add(tf.nn.conv2d\ (_input_r, _W['ce1'],\ strides=[1, 2, 2, 1],\ padding='SAME'),\ _b['be1'])) ``` 在移動到第二個卷積層之前，我們應用了丟棄操作： ```py _ce1 = tf.nn.dropout(_ce1, _keepprob) ``` 在下面的兩個編碼層中，我們應用相同的卷積和丟棄操作： ```py _ce2 = tf.nn.sigmoid\ (tf.add(tf.nn.conv2d\ (_ce1, _W['ce2'],\ strides=[1, 2, 2, 1],\ padding='SAME'),\ _b['be2'])) _ce2 = tf.nn.dropout(_ce2, _keepprob) _ce3 = tf.nn.sigmoid\ (tf.add(tf.nn.conv2d\ (_ce2, _W['ce3'],\ strides=[1, 2, 2, 1],\ padding='SAME'),\ _b['be3'])) _ce3 = tf.nn.dropout(_ce3, _keepprob) ``` 特征數量從 1（輸入圖像）增加到 64，而原始形狀圖像已減少到`28×28`到`7×7`。在解碼階段，壓縮（或編碼）和重新成形的圖像必須為盡可能與原始圖像相似。為實現這一目標，我們在接下來的三個層中使用了`conv2d_transpose` TensorFlow 函數： ```py tf.nn.conv2d_transpose(value, filter, output_shape, strides, padding='SAME') ``` 這種操作有時是 ，稱為反卷積；它只是`conv2d`的梯度。該函數的參數如下： * `value`：`float`型和形狀`[batch, height, width, in_channels]`的 4D 張量。 * `filter`：與`value`和形狀`[height, width, output_channels, in_channels]`具有相同類型的 4D 張量。`in_channels`維度必須與值匹配。 * `output_shape`：表示去卷積操作的輸出形狀的 1D 張量。 * `strides`：整數列表。輸入張量的每個維度的滑動窗口的步幅。 * `padding`：一個有效的字符串或`SAME`。 `conv2d_transpose`函數將返回與`value`參數類型相同的張量。第一個去卷積層`_cd3`具有卷積層`_ce3`作為輸入。它返回`_cd3`張量，其形狀為`(1,7,7,32)`： ```py _cd3 = tf.nn.sigmoid\ (tf.add(tf.nn.conv2d_transpose\ (_ce3, _W['cd3'],\ tf.stack([tf.shape(_X)[0], 7, 7, n2]),\ strides=[1, 2, 2, 1],\ padding='SAME'),\ _b['bd3'])) _cd3 = tf.nn.dropout(_cd3, _keepprob) ``` 對于第二個去卷積層`_cd2`，我們將反卷積層`_cd3`作為輸入傳遞。它返回`_cd2`張量，其形狀為`(1,14,14,16)`： ```py _cd2 = tf.nn.sigmoid\ (tf.add(tf.nn.conv2d_transpose\ (_cd3, _W['cd2'],\ tf.stack([tf.shape(_X)[0], 14, 14, n1]),\ strides=[1, 2, 2, 1],\ padding='SAME'),\ _b['bd2'])) _cd2 = tf.nn.dropout(_cd2, _keepprob) ``` 第三個也是最后一個反卷積層`_cd1`將`_cd2`層作為輸入傳遞。它返回結果`_out`張量，其形狀為`(1,28,28,1)`，與輸入圖像相同： ```py _cd1 = tf.nn.sigmoid\ (tf.add(tf.nn.conv2d_transpose\ (_cd2, _W['cd1'],\ tf.stack([tf.shape(_X)[0], 28, 28, 1]),\ strides=[1, 2, 2, 1],\ padding='SAME'),\ _b['bd1'])) _cd1 = tf.nn.dropout(_cd1, _keepprob) _out = _cd1 return _out ``` 然后我們將成本函數定義為`y`和`pred`之間的均方誤差： ```py pred = cae(x, weights, biases, keepprob) cost = tf.reduce_sum\ (tf.square(cae(x, weights, biases, keepprob)\ - tf.reshape(y, shape=[-1, 28, 28, 1]))) learning_rate = 0.001 ``` 為了優化成本，我們將使用`AdamOptimizer`： ```py optm = tf.train.AdamOptimizer(learning_rate).minimize(cost) ``` 在下一步中，我們配置我們的網絡來運行會話： ```py init = tf.global_variables_initializer() print ("Functions ready") sess = tf.Session() sess.run(init) mean_img = np.zeros((784)) ``` 批次的大小設置為`128`： ```py batch_size = 128 ``` 周期數是`50`： ```py n_epochs = 50 ``` 然后我們開始循環會話： ```py for epoch_i in range(n_epochs): ``` 對于每個周期，我們得到一個批量集`trainbatch`： ```py for batch_i in range(mnist.train.num_examples // batch_size): batch_xs, _ = mnist.train.next_batch(batch_size) trainbatch = np.array([img - mean_img for img in batch_xs]) ``` 我們應用隨機噪聲，就像去噪自編碼器一樣，來改善學習： ```py trainbatch_noisy = trainbatch + 0.3*np.random.randn(\ trainbatch.shape[0], 784) sess.run(optm, feed_dict={x: trainbatch_noisy \ , y: trainbatch, keepprob: 0.7}) print ("[%02d/%02d] cost: %.4f" % (epoch_i, n_epochs \ , sess.run(cost, feed_dict={x: trainbatch_noisy \ , y: trainbatch, keepprob: 1.}))) ``` 對于每個訓練周期，我們隨機抽取五個訓練樣例： ```py if (epoch_i % 10) == 0: n_examples = 5 test_xs, _ = mnist.test.next_batch(n_examples) test_xs_noisy = test_xs + 0.3*np.random.randn( test_xs.shape[0], 784) ``` 然后我們在一個小子集上測試訓練模型： ```py recon = sess.run(pred, feed_dict={x: test_xs_noisy,\ keepprob: 1.}) fig, axs = plt.subplots(2, n_examples, figsize=(15, 4)) for example_i in range(n_examples): axs[0][example_i].matshow(np.reshape( test_xs_noisy[example_i, :], (28, 28)) , cmap=plt.get_cmap('gray')) ``` 最后，我們可以使用 Matplotlib 顯示輸入和學習集： ```py axs[1][example_i].matshow(np.reshape( np.reshape(recon[example_i, ...], (784,)) + mean_img, (28, 28)), cmap=plt.get_cmap('gray')) plt.show() ``` 執行將產生以下輸出： ```py >>> Extracting data/train-images-idx3-ubyte.gz Extracting data/train-labels-idx1-ubyte.gz Extracting data/t10k-images-idx3-ubyte.gz Extracting data/t10k-labels-idx1-ubyte.gz Packages loaded Network ready Functions ready Start training.. [00/05] cost: 8049.0332 [01/05] cost: 3706.8667 [02/05] cost: 2839.9155 [03/05] cost: 2462.7021 [04/05] cost: 2391.9460 >>> ``` 請注意，對于每個周期，我們將可視化輸入集和先前顯示的相應學習集。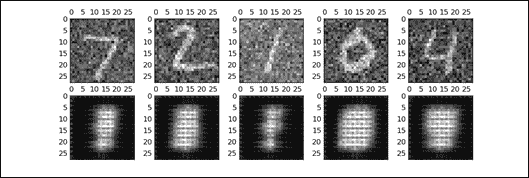正如您在第一個周期所看到的，我們不知道哪些圖像已被學習：  圖 11：第一個周期圖像 在第二個周期， 的想法變得更加清晰 ：  圖 12：第二周期圖像 這是第三個周期：  圖 13：第三周期圖像 在第四個周期再好一點：  圖 14：第四周期圖像 我們可能已經停止在上一個周期，但這是第五個也是最后一個周期：  圖 15：第五周期圖像 到目前為止，我們已經看到了自編碼器的不同實現以及改進版本。但是，將此技術應用于 MNIST 數據集并不能說明其真正的力量。因此，現在是時候看到一個更現實的問題，我們可以應用自編碼器技術。 # 自編碼器和欺詐分析 銀行，保險公司和信用合作社等金融公司的欺詐檢測和預防是一項重要任務。到目前為止，我們已經看到如何以及在何處使用深度神經網絡（DNN） 和卷積神經網絡（CNN）。 現在是時候使用其他無監督學習算法，如自編碼器。在本節中，我們將探索信用卡交易的數據集，并嘗試構建一個無監督的機器學習模型，該模型能夠判斷特定交易是欺詐性的還是真實的。 更具體地說，我們將使用自編碼器預先訓練分類模型并應用異常檢測技術來預測可能的欺詐。在開始之前，我們需要知道數據集。 ## 數據集的描述 對于這個例子，我們將使用來自 Kaggle 的信用卡欺詐檢測數據集。數據集可以從[此鏈接](https://www.kaggle.com/hunk3749/credit-card/data)下載。由于我使用的是數據集，因此引用以下出版物時，最好是透明的： Andrea Dal Pozzolo，Olivier Caelen，Reid A. Johnson 和 Gianluca Bontempi。用不平衡分類的欠采樣校準概率。在計算智能和數據挖掘研討會（CIDM），IEEE，2015 年。 該數據集包含 2013 年 9 月歐洲信用卡持有人在兩天內進行的交易。共有 285,299 筆交易，只有 492 筆欺詐，這意味著數據集非常不平衡。正類（欺詐）占所有交易的 0.172%。 數據集包含數字輸入變量，這些變量是 PCA 轉換的結果。遺憾的是，由于機密性問題，我們無法提供有關數據的原始特征和更多背景信息。有 28 個特征，即`V1`，`V2`，... `V27`，它們是使用 PCA 獲得的主要成分，除了`Time`和`Amount`特征。`Class`特征是響應變量，在欺詐情況下取值`1`，否則取`0`。 還有兩個附加特征，`Time`和`Amount`。`Time`列表示每筆交易與第一筆交易之間的時間（以秒為單位），而`Amount`列表示此交易中轉賬的金額。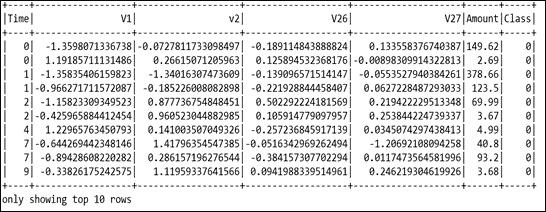那么，讓我們看一下輸入數據（僅顯示`V1`，`V2`，`V26`和`V27`），如圖 16 所示：  圖 16：信用卡欺詐檢測數據集的快照 ## 問題描述 對于這個例子，我們將使用自編碼器作為無監督的特征學習算法，該算法學習和概括訓練數據共享的公共模式。在重建階段，對于具有異常模式的數據點，RMSE 將更高。因此，這些數據點是異常值或異常值。我們的假設是，異常也等于我們所追求的欺詐性交易。 現在，在評估步驟中，我們可以根據驗證數據選擇 RMSE 的閾值，并將 RMSE 高于閾值的所有數據標記為欺詐。或者，如果我們認為 0.1% 的交易都是欺詐性的，我們也可以根據每個數據點（即 RMSE）的重建誤差對數據進行排名，然后選擇前 0.1% 為欺詐性交易。 給定類不平衡比，建議使用精確回憶曲線下面積（AUPRC）測量精度 ，因為混淆矩陣精度在不平衡分類中沒有意義。在這種情況下，使用線性機器學習模型，例如隨機森林，邏輯回歸或支持向量機，通過應用上下采樣技術，將是一個更好的主意。或者，我們可以嘗試查找數據中的異常，因為我們假設數據集中只有少數欺詐案例，即異常。 在處理如此嚴重的響應標簽不平衡時，我們在測量模型表現時也需要小心。只有少數欺詐性實例，因此將一切預測為非欺詐的模型將達到 99% 以上的準確率。然而，盡管它們具有高精度，但線性 ML 模型（甚至是樹組合）并不一定能幫助我們找到欺詐性案例。 對于這個例子，我們將構建一個無監督的模型：該模型將接受正面和負面數據（欺詐和非欺詐）的訓練，但不提供標簽。由于我們有比欺詐更多的正常交易，我們應該期望該模型在訓練后學習和記憶正常交易的模式，并且該模型應該能夠為任何異常交易給出分數。 這種無監督的訓練對于此目的非常有用，因為我們沒有足夠的標記數據。那么，讓我們開始吧。 ## 探索性數據分析 在我們實現模型之前，探索數據集將提供一些見解。我們首先導入所需的包和模塊（包括此示例所需的其他包）和模塊： ```py import pandas as pd import numpy as np import tensorflow as tf import os from datetime import datetime from sklearn.metrics import roc_auc_score as auc import seaborn as sns # for statistical data visualization import matplotlib.pyplot as plt import matplotlib.gridspec as gridspec ``` ### 提示 安裝 seaborn 您可以通過多種方式安裝`seaborn`，這是一個用于統計數據可視化的 Python 模塊： ```py $ sudo pip install seaborn # for Python 2.7 $ sudo pip3 install seaborn # for Python 3.x $ sudo conda install seaborn # using conda # Directly from GitHub (use pip for Python 2.7) $ pip3 install git+https://github.com/mwaskom/seaborn.git ``` 現在，[我假設您已經從上述 URL 下載了數據集](https://www.kaggle.com/hunk3749/credit-card/data)。下載附帶一個名為`creditcard.csv`的 CSV 文件。 接下來，讓我們閱讀數據集并創建一個 pandas `DataFrame`： ```py df = pd.read_csv('creditcard.csv') print(df.shape) >>> (284807, 31) ``` 因此，數據集具有關于 300,000 個事務，30 個特征和兩個二元標簽（即 0/1）。現在讓我們看一下列名及其數據類型： ```py print(df.columns) >>> Index(['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10', 'V11', 'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20', 'V21', 'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'Amount', 'Class'], dtype='object') print(df.dtypes) >>> Time float64 V1 float64 V2 float64 V3 float64 … V25 float64 V26 float64 V27 float64 V28 float64 Amount float64 Class int64 ``` 現在讓我們來看看數據集： ```py print(df.head()) >>> ```  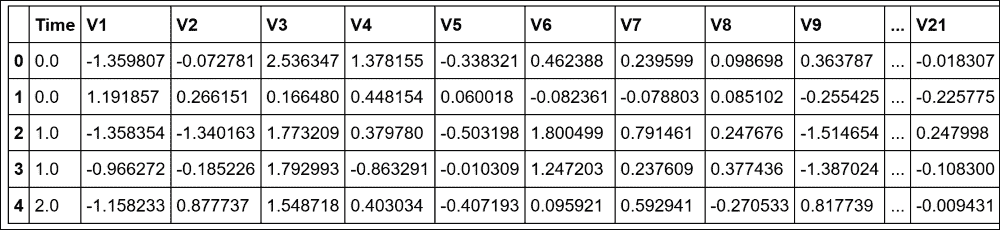圖 17：數據集的快照 現在讓我們看看所有交易的時間跨度： ```py print("Total time spanning: {:.1f} days".format(df['Time'].max() / (3600 * 24.0))) >>> Total time spanning: 2.0 days ``` 現在讓我們看看這些類的統計信息： ```py print("{:.3f} % of all transactions are fraud. ".format(np.sum(df['Class']) / df.shape[0] * 100)) >>> 0.173 % of all transactions are fraud. ``` 因此，我們只有少數欺詐交易。這在文獻中也被稱為罕見事件檢測，并且意味著數據集高度不平衡。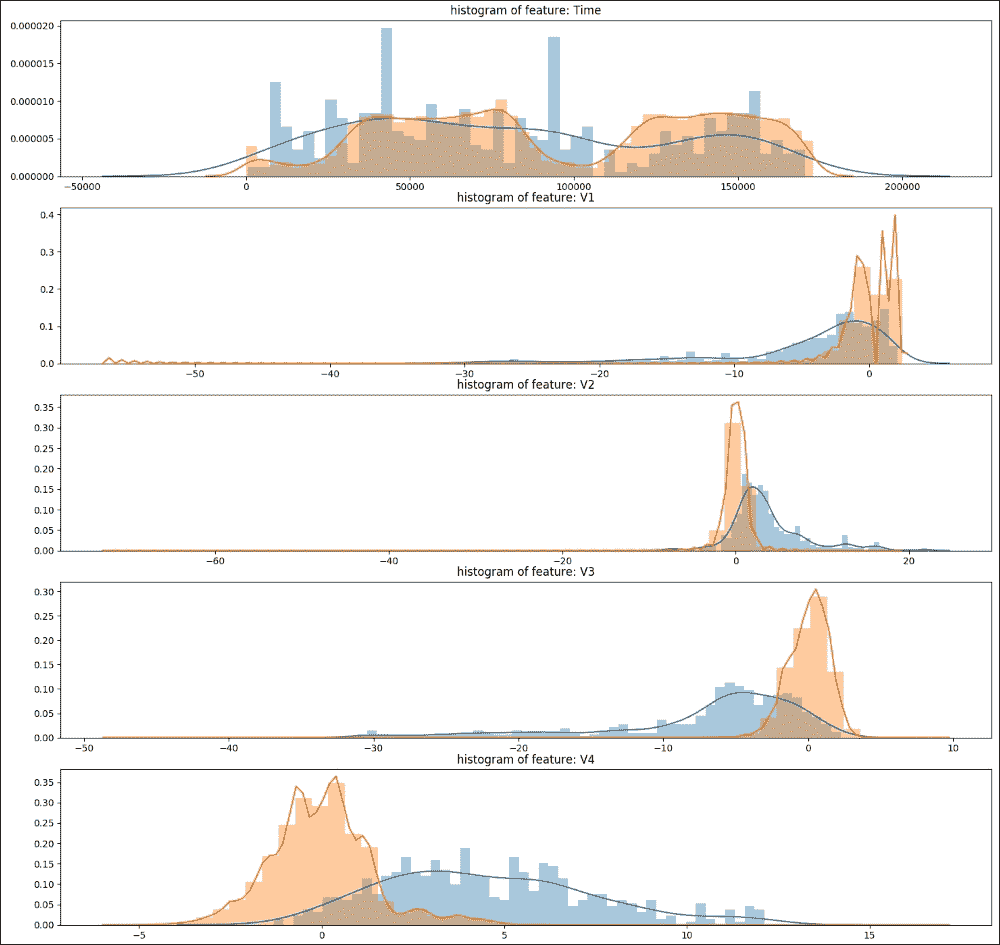現在，讓我們繪制前五個特征的直方圖： ```py plt.figure(figsize=(12,5*4)) gs = gridspec.GridSpec(5, 1) for i, cn in enumerate(df.columns[:5]): ax = plt.subplot(gs[i]) sns.distplot(df[cn][df.Class == 1], bins=50) sns.distplot(df[cn][df.Class == 0], bins=50) ax.set_xlabel('') ax.set_title('histogram of feature: ' + str(cn)) plt.show() >>> ```  圖 18：顯示前五個特征的直方圖 在前面的屏幕截圖中，可以看出所有特征都是正偏差或負偏斜。此外，數據集沒有很多特征，因此修剪尾部會丟失重要的信息。所以，暫時，讓我們盡量不這樣做，并使用所有特征。 ## 訓練，驗證和測試集準備 讓我們通過將數據分成訓練，開發（也稱為驗證）和測試集來開始訓練。我們首先使用 80% 的數據作為訓練和驗證集。剩余的 20% 將用作測試集： ```py TEST_RATIO = 0.20 df.sort_values('Time', inplace = True) TRA_INDEX = int((1-TEST_RATIO) * df.shape[0]) train_x = df.iloc[:TRA_INDEX, 1:-2].values train_y = df.iloc[:TRA_INDEX, -1].values test_x = df.iloc[TRA_INDEX:, 1:-2].values test_y = df.iloc[TRA_INDEX:, -1].values ``` 現在，讓我們對前面的分裂進行統計： ```py print("Total train examples: {}, total fraud cases: {}, equal to {:.5f} % of total cases. ".format(train_x.shape[0], np.sum(train_y), (np.sum(train_y)/train_x.shape[0])*100)) print("Total test examples: {}, total fraud cases: {}, equal to {:.5f} % of total cases. ".format(test_x.shape[0], np.sum(test_y), (np.sum(test_y)/test_y.shape[0])*100)) >>> Total train examples: 227845, total fraud cases: 417, equal to 0.18302 % of total cases. Total test examples: 56962, total fraud cases: 75, equal to 0.13167 % of total cases. ``` ## 歸一化 為了獲得更好的預測準確率，我們可以考慮兩種類型的標準化：z 得分和 min-max 縮放： * Z 得分：這將每列歸一化為零均值并將其標準化。這特別適用于激活函數，例如 tanh，其輸出零兩側的值。其次，這將留下極端值，因此在正常化之后會有一些極端。在這種情況下，這可能對檢測異常值很有用。 * 最小 - 最大縮放：這確保所有值都在 0 和 1 之間，即正數。如果我們使用 sigmoid 作為輸出激活，這是默認方法。 我們使用驗證集來決定數據標準化方法和激活函數。根據實驗，我們發現當與 z 得分標準化一起使用時，tanh 的表現略好于 sigmoid。因此，我們選擇了 tanh，然后是 z 得分： ```py cols_mean = [] cols_std = [] for c in range(train_x.shape[1]): cols_mean.append(train_x[:,c].mean()) cols_std.append(train_x[:,c].std()) train_x[:, c] = (train_x[:, c] - cols_mean[-1]) / cols_std[-1] test_x[:, c] = (test_x[:, c] - cols_mean[-1]) / cols_std[-1] ``` ## 作為無監督特征學習算法的自編碼器 在本小節中，我們將看到如何使用自編碼器作為無監督的特征學習算法。首先，讓我們初始化網絡超參數： ```py learning_rate = 0.001 training_epochs = 1000 batch_size = 256 display_step = 10 n_hidden_1 = 15 # number of neurons is the num features n_input = train_x.shape[1] ``` 由于第一層和第二層分別包含 15 和 5 個神經元，我們正在構建這樣的架構網絡：28（輸入）-> 15 -> 5 -> 15 -> 28（輸出）。那么讓我們構建我們的自編碼器網絡。 讓我們創建一個 TensorFlow 占位符來保存輸入： ```py X = tf.placeholder("float", [None, n_input]) ``` 現在我們必須使用隨機初始化創建偏差和權重向量： ```py weights = { 'encoder_h1': tf.Variable\ (tf.random_normal([n_input, n_hidden_1])), 'decoder_h1': tf.Variable\ (tf.random_normal([n_hidden_1, n_input])), } biases = { 'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])), 'decoder_b1': tf.Variable(tf.random_normal([n_input])), } ``` 現在，我們構建一個簡單的自編碼器。這里我們有`encoder()`函數，它構造了編碼器。我們使用`tanh`函數對隱藏層進行編碼，如下所示： ```py def encoder(x): layer_1 = tf.nn.tanh(tf.add\ (tf.matmul(x, weights['encoder_h1']),\ biases['encoder_b1'])) return layer_1 ``` 這是`decoder()`函數，它構造了解碼器。我們使用`tanh`函數解碼隱藏層，如下所示： ```py def decoder(x): layer_1 = tf.nn.tanh(tf.add\ (tf.matmul(x, weights['decoder_h1']),\ biases['decoder_b1'])) return layer_1 ``` 之后，我們通過傳遞輸入數據的 TensorFlow 占位符來構建模型。權重和偏置（NN 的`W`和`b`）包含我們將學習優化的網絡的所有參數，如下所示： ```py encoder_op = encoder(X) decoder_op = decoder(encoder_op) ``` 一旦我們構建了自編碼器網絡，就可以進行預測，其中目標是輸入數據： ```py y_pred = decoder_op y_true = X ``` 現在我們已經進行了預測，現在是時候定義`batch_mse`來評估表現： ```py batch_mse = tf.reduce_mean(tf.pow(y_true - y_pred, 2), 1) ``` ### 注意 未觀測值的均方誤差（MSE）是[平方誤差](https://en.wikipedia.org/wiki/Errors_and_residuals)或[偏差](https://en.wikipedia.org/wiki/Deviation_(statistics))的[平均值](https://en.wikipedia.org/wiki/Expected_value)。從統計學的角度來看， 它是估計量質量的度量（它總是非負的，接近于零的值更好）。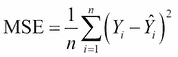 如果`Y^`是 n 個預測的向量，并且`Y`是被預測變量的觀測值的向量，則預測變量的樣本內 MSE 計算如下：  因此，MSE 是誤差平方`(Y[i] - Y^[i])^2`的平均值`(1/n ∑[i])`。 我們在這里有另一個`batch_mse`將返回批量中所有輸入數據的 RMSE，這是一個長度等于輸入數據中行數的向量。如果您想要輸入（無論是訓練，驗證還是測試數據），這些將是預測值或欺詐分數，我們可以在預測后提取出來。然后我們定義損失和優化器，并最小化平方誤差： ```py cost_op = tf.reduce_mean(tf.pow(y_true - y_pred, 2)) optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(cost_op) ``` 每層所用的激活函數是`tanh`。這里的目標函數或成本測量一批中預測和輸入數組的總 RMSE，這意味著它是一個標量。然后，每次我們想要進行批量更新時，我們都會運行優化器。 太棒了！我們準備開始訓練了。但是，在此之前，讓我們定義保存訓練模型的路徑： ```py save_model = os.path.join(data_dir, 'autoencoder_model.ckpt') saver = tf.train.Saver() ``` 到目前為止，我們已經定義了許多變量以及超參數，因此我們必須初始化變量： ```py init_op = tf.global_variables_initializer() ``` 最后，我們開始訓練。我們在訓練周期中循環所有批次。然后我們運行優化操作和成本操作來獲得損失值。然后我們顯示每個周期步驟的日志。最后，我們保存訓練有素的模型： ```py epoch_list = [] loss_list = [] train_auc_list = [] data_dir = 'Training_logs/' with tf.Session() as sess: now = datetime.now() sess.run(init_op) total_batch = int(train_x.shape[0]/batch_size) # Training cycle for epoch in range(training_epochs): # Loop over all batches for i in range(total_batch): batch_idx = np.random.choice(train_x.shape[0],\ batch_size) batch_xs = train_x[batch_idx] # Run optimization op (backprop) and # cost op (to get loss value) _, c = sess.run([optimizer, cost_op],\ feed_dict={X: batch_xs}) # Display logs per epoch step if epoch % display_step == 0: train_batch_mse = sess.run(batch_mse,\ feed_dict={X: train_x}) epoch_list.append(epoch+1) loss_list.append(c) train_auc_list.append(auc(train_y, train_batch_mse)) print("Epoch:", '%04d,' % (epoch+1), "cost=", "{:.9f},".format(c), "Train auc=", "{:.6f},".format(auc(train_y, \ train_batch_mse)), print("Optimization Finished!") save_path = saver.save(sess, save_model) print("Model saved in: %s" % save_path) save_model = os.path.join(data_dir, autoencoder_model_1L.ckpt') saver = tf.train.Saver() ``` 前面的代碼段很簡單。每次，我們從`train_x`中隨機抽取 256 個小批量的小批量，作為`X`的輸入將其輸入模型，并運行優化器通過隨機梯度下降更新參數 SGD）： ```py >>> Epoch: 0001, cost= 0.938937187, Train auc= 0.951383 Epoch: 0011, cost= 0.491790086, Train auc= 0.954131 … Epoch: 0981, cost= 0.323749095, Train auc= 0.953185 Epoch: 0991, cost= 0.255667418, Train auc= 0.953107 Optimization Finished! Model saved in: Training_logs/autoencoder_model.ckpt Test auc score: 0.947296 ``` 我們在`train_x`上的估值得出的 AUC 得分約為 0.95。然而，從前面的日志中，很難理解訓練的進展情況： ```py # Plot Training AUC over time plt.plot(epoch_list, train_auc_list, 'k--', label='Training AUC', linewidth=1.0) plt.title('Training AUC per iteration') plt.xlabel('Iteration') plt.ylabel('Training AUC') plt.legend(loc='upper right') plt.grid(True) # Plot train loss over time plt.plot(epoch_list, loss_list, 'r--', label='Training loss', linewidth=1.0) plt.title('Training loss') plt.xlabel('Iteration') plt.ylabel('Loss') plt.legend(loc='upper right') plt.grid(True) plt.show() >>> ```  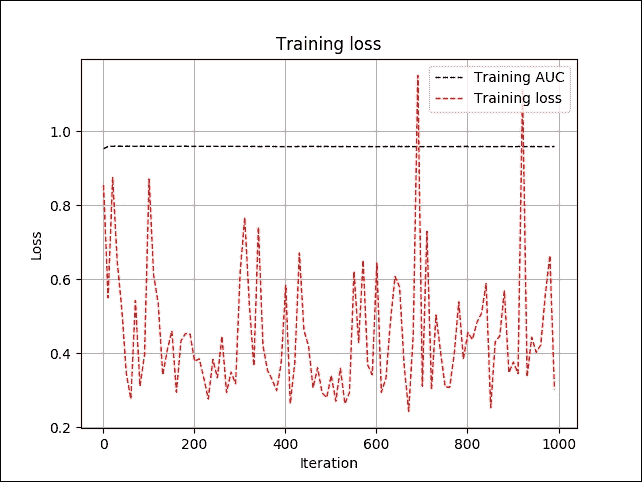圖 19：每次迭代的訓練損失和 AUC 在上圖中，我們可以看到訓練誤差有點顛簸，但訓練 AUC 幾乎保持穩定，約為 95%。這可能聽起來很可疑。您還可以看到我們使用相同的數據進行訓練和驗證。這可能聽起來很混亂，但等等！ 由于我們正在進行無監督的訓練，并且模型在訓練期間從未看到標簽，因此不會導致過擬合。此附加驗證用于監視早期停止以及超參數調整。 ## 評估模型 在訓練完我們的自編碼器模型和超參數后，我們可以在 20% 測試數據集上評估其表現，如下所示： ```py save_model = os.path.join(data_dir, autoencoder_model.ckpt') saver = tf.train.Saver() # Initializing the variables init = tf.global_variables_initializer() with tf.Session() as sess: now = datetime.now() saver.restore(sess, save_model) test_batch_mse = sess.run(batch_mse, feed_dict={X: test_x}) print("Test auc score: {:.6f}".format(auc(test_y, \ test_batch_mse))) ``` 在此代碼中，我們重用了之前制作的訓練模型。`test_batch_mse`是我們測試數據的欺詐分數： ```py >>> Test auc score: 0.948843 ``` 太棒了！我們訓練有素的模型被證明是一個高度準確的模型，顯示 AUC 約為 95%。現在我們已經看到了評估，一些可視化分析會很棒。你們覺得怎么樣？讓我們繪制非欺詐案件的欺詐分數（MSE）分布圖。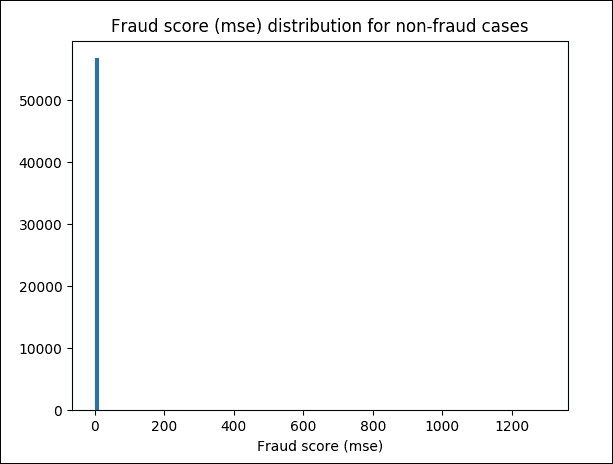以下代碼段執行此操作： ```py plt.hist(test_batch_mse[test_y == 0.0], bins = 100) plt.title("Fraud score (mse) distribution for non-fraud cases") plt.xlabel("Fraud score (mse)") plt.show() >>> ```  圖 20：非欺詐案件的 MSE 欺詐評分 前面的屏幕截圖是不可理解的，所以讓我們將其縮放到`(0, 30)`范圍并再次繪制圖形： ```py # Zoom into (0, 30) range plt.hist(test_batch_mse[(test_y == 0.0) & (test_batch_mse < 30)], bins = 100) plt.title("Fraud score (mse) distribution for non-fraud cases") plt.xlabel("Fraud score (mse)") plt.show() >>> ```  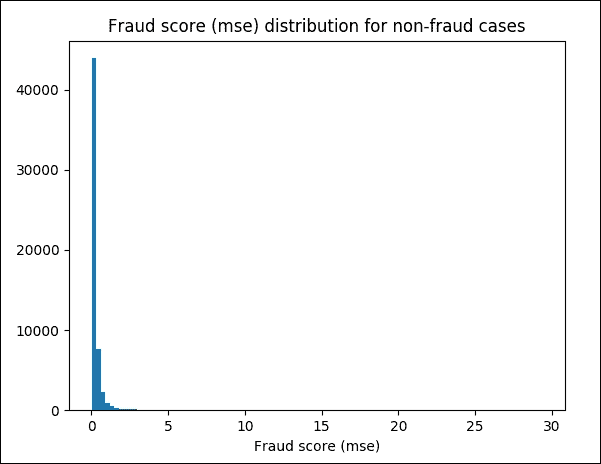圖 21：非欺詐案件的 MSE 欺詐評分，放大到`(0, 30)`范圍 現在讓我們只顯示欺詐類： ```py # Display only fraud classes plt.hist(test_batch_mse[test_y == 1.0], bins = 100)plt.title("Fraud score (mse) distribution for fraud cases") plt.xlabel("Fraud score (mse)") plt.show() >>> ```  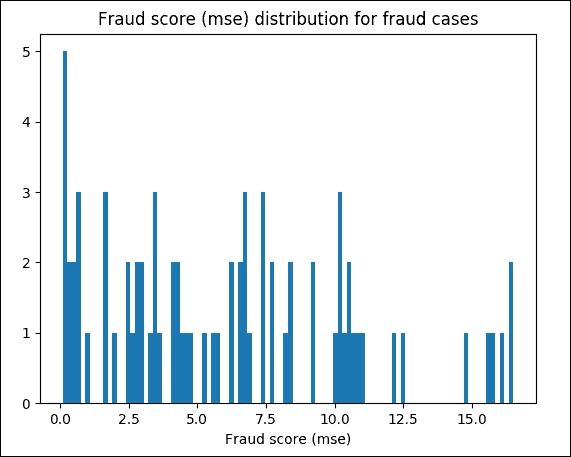圖 22：欺詐案件的 MSE 欺詐評分 最后，讓我們看一下一些相關統計數據。例如，我們使用`10`作為檢測閾值。現在我們可以計算高于閾值的檢測到的病例數，高于閾值的陽性病例數，高于閾值的準確率百分比（即精確度），并將其與測試集中欺詐的平均百分比進行比較： ```py threshold = 10 print("Number of detected cases above threshold: {}, \n\ Number of pos cases only above threshold: {}, \n\ The percentage of accuracy above threshold (Precision): {:0.2f}%. \n\ Compared to the average percentage of fraud in test set: 0.132%".format( \ np.sum(test_batch_mse > threshold), \ np.sum(test_y[test_batch_mse > threshold]), \ np.sum(test_y[test_batch_mse > threshold]) / np.sum(test_batch_mse > threshold) * 100)) >>> Number of detected cases above threshold: 198, Number of positive cases only above threshold: 18, The percentage of accuracy above threshold (Precision): 9.09%. Compared to the average percentage of fraud in test set: 0.132% ``` 總而言之，對于我們的案例，只有一個隱藏層的自編碼器足夠（至少用于訓練）。但是，您仍然可以嘗試采用其他變體，例如解卷積自編碼器和去噪自編碼器來解決同樣的問題。 # 總結 在本章中，我們實現了一些稱為自編碼器的優化網絡。自編碼器基本上是數據壓縮網絡模型。它用于將給定輸入編碼為較小維度的表示，然后可以使用解碼器從編碼版本重建輸入。我們實現的所有自編碼器都包含編碼和解碼部分。 我們還看到了如何通過在網絡訓練期間引入噪聲和構建去噪自編碼器來提高自編碼器的表現。最后，我們應用第 4 章中介紹的 CNN 概念，卷積神經網絡上的 TensorFlow 和卷積自編碼器的實現。 即使隱藏單元的數量很大，我們仍然可以通過在網絡上施加其他約束來使用自編碼器發現數據集的有趣和隱藏結構。換句話說，如果我們對隱藏單元施加稀疏約束，那么即使隱藏單元的數量很大，自編碼器仍將在數據中發現有趣的結構。為了證明這一觀點，我們看到了一個真實的例子，即信用卡欺詐分析，我們成功應用了自編碼器。 循環神經網絡（RNN）是一類人工神經網絡，其中單元之間的連接形成有向循環。 RNN 利用過去的信息，如時間序列預測。這樣，他們就可以對具有高時間依賴性的數據進行預測。這創建了網絡的內部狀態，允許它展示動態時間行為。 在下一章中，我們將研究 RNN。我們將首先描述這些網絡的基本原理，然后我們將實現這些架構的一些有趣示例。