背包問題：動態編程示例 · Guru99 中文系列教程

# 背包問題：動態編程示例 > 原文： [https://www.guru99.com/knapsack-problem-dynamic-programming.html](https://www.guru99.com/knapsack-problem-dynamic-programming.html) ## 什么是背包問題？ **背包問題**是組合學中非常有用的問題。在超級市場中，有 n 個包裹（n≤100），包裹 i 的重量 W [i]≤100，值 V [i]≤100。小偷闖入超級市場，小偷不能攜帶超過 M 的重量（M≤100 ）。這里要解決的問題是：小偷將帶走哪些包裝以獲得最高價值？輸入： * 最大重量 M 和包裹數 n。 * 權重 W [i]和對應值 V [i]的數組。輸出： * 最大化價值和相應的容量。 * 小偷將帶走哪些包裹。背包問題可以進一步分為兩種類型： * 0/1 背包問題。在這種類型的情況下，每個包裹都可以被取走或不被取走。此外，小偷不能拿走一小部分的包裹，也不能多次拿走一個包裹。這種類型可以通過動態編程方法解決。 * 小背包問題。這種類型可以通過貪婪策略來解決。在本教程中，您將學習： * [什么是背包問題？](#1) * [動態編程簡介](#2) * [分析 0/1 背包問題](#3) * [計算 B [i] [j]](#4) 的公式 * [動態編程的基礎](#5) * [計算選項表](#6) * [跡線 5](#7) * [查找選項表以查找所選軟件包的算法](#8) * [Java 代碼](#9) ## 動態編程簡介在分而治之的策略中，您將要解決的問題分為多個子問題。子問題進一步分為較小的子問題。該任務將繼續進行，直到您遇到可以輕松解決的子問題為止。但是，在這種劃分過程中，您可能會多次遇到相同的問題。動態編程的基本思想是使用表格來存儲已解決子問題的解決方案。如果再次遇到子問題，則只需將表中的解決方案作為解決方案，而不必再次解決。因此，通過動態編程設計的算法非常有效。 ![](https://img.kancloud.cn/cd/9d/cd9d0b9a89438da94f3646abafe0b2bd_659x123.png) 要通過動態編程解決問題，您需要執行以下任務： * 查找最小子問題的解決方案。 * 找出公式（或規則），以通過甚至最小的子問題的解決方案來構建子問題的解決方案。 * 創建一個表來存儲子問題的解決方案。然后根據找到的公式計算子問題的解并保存到表中。 * 從已解決的子問題中，您可以找到原始問題的解決方案。 ## 分析 0/1 背包問題分析此類型時，您會發現一些值得注意的地方。背包算法的價值取決于兩個因素： 1. 正在考慮多少個包裹 2. 背包可以存放的剩余重量。因此，您有兩個可變數量。通過動態編程，您可以獲得有用的信息： 1. 目標函數將取決于兩個變量 2. 選項表將是一個二維表。如果通過選擇權重限制為 j 的軟件包{1、2，...，i}來調用 B [i] [j]是最大可能值。 * 在重量限制為 M 的 n 個包裝中選擇的最大值是 B [n] [M]。換句話說：當有 i 個包裹可供選擇時，B [i] [j]是背包的最大重量為 j 時的最佳重量。 * 最佳權重始終小于或等于最大權重：B [i] [j]≤j。例如：B [4] [10] =8。這表示在最佳情況下，當有 4 個第一包裝供您選擇（第一至第四包裝）時，所選包裝的總重量為 8，最大重量為背包的最大數量是 10。不必全部選擇 4 個項目。 ## 計算 B [i] [j]的公式輸入，您定義： * W [i]，V [i]依次是包裝 i 的重量和值，其中 i [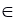![](https://img.kancloud.cn/89/76/8976a16447bcd54a292d0ce04f5cace2_16x23.png) ](/images/1/043019_0611_KnapsackPro4.png) {1，…，n}。 * M 是背包的最大重量。如果僅選擇一個包。您為每個 j 計算 B [1] [j]：這意味著背包的最大重量≥第一個包裝的重量 ``` B[1][j] = W[1] ``` 在權重限制為 j 的情況下，程序包{1,2，...，i – 1，i}中具有最大值的最佳選擇將有兩種可能性： * 如果未選擇包裝 i，則通過在重量限制為 j 的包裝{1、2，...，i – 1}中進行選擇，B [i] [j]是最大可能值。你有： ``` B[i][j] = B[i – 1][j] ``` * 如果選擇了程序包 i（當然，僅當 W [i]≤j 時才考慮這種情況），則 B [i] [j]等于程序包 i 的值 V [i]加最大值可以通過選擇包裝{1、2，...，i – 1}，重量限制為（j – W [i]）。也就是說，就您所擁有的價值而言： ``` B[i][j] = V[i] + B[i – 1][j – W[i]] ``` 由于創建了 B [i] [j]（這是可能的最大值），因此 B [i] [j]將是上述 2 個值中的最大值。 ## 動態編程的基礎因此，您必須考慮選擇包 i 是否更好。從那里，您具有如下的遞歸公式： ``` B[i][j]= max(B[i – 1][j], V[i]+B[i – 1][j – W[i]] ``` 很容易看出 B [0] [j] =最大值，可以從 0 包= 0 中進行選擇。 ## 計算選項表您基于上述遞歸公式構建一個選項表。要檢查結果是否正確（如果不完全正確，則重建目標函數 B [i] [j]）。通過創建目標函數 B [i] [j]和選項表，可以確定跟蹤的方向。選項表 B 包含 n + 1 行，M + 1 列， * 首先，填充動態編程的基礎：第 0 行包含所有零。 * 使用遞歸公式，使用第 0 行計算第 1 行，使用第 1 行計算第 2 行，依此類推...直到計算出所有行。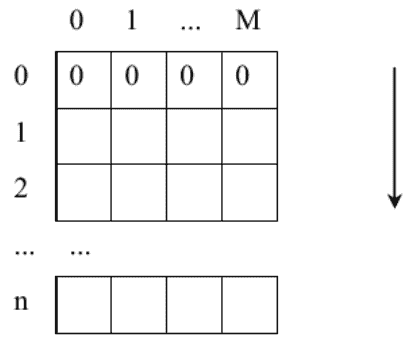 <figure style="margin-left: auto;margin-right: auto;"> ![](https://img.kancloud.cn/f3/a7/f3a7c6c8bc625caec463fd5c6d66762e_414x343.png) Table of Options ## 跟蹤在計算選項表時，您對 B [n] [M]感興趣，B [n] [M]是在所有 n 個重量限制為 M 的包裝中進行選擇時獲得的最大值。 * 如果 **B [n] [M] = B [n – 1] [M]** ，則未選擇包 n，則跟蹤 B [n – 1] [M]。 * 如果 **B [n] [M]≠B [n – 1] [M]** ，則您會注意到最佳選擇具有包 n 和跡線 B [n – 1] [M – W [n] ]。繼續跟蹤，直到到達選項表的第 0 行。 ## 查找選項表以查找所選軟件包的算法注意：如果 B [i] [j] = B [i – 1] [j]，則不選擇包 i。 B [n] [W]是放入背包的包裹的最佳總價值。跟蹤步驟： * **步驟 1** ：從 i = n，j = M 開始。 * **步驟 2** ：從底部向上看 j 列，找到第 i 行，使得 B [i] [j] > B [i – 1] [j]。標記選中的程序包 i：選擇[i] = true； * **步驟 3** ：j = B [i] [j] – W [i]。如果 j > 0，請轉到步驟 2，否則請轉到步驟 4 * **步驟 4** ：基于選項表來打印選定的軟件包。 ## Java 代碼 ``` public void knapsackDyProg(int W[], int V[], int M, int n) { int B[][] = new int[n + 1][M + 1]; for (int i=0; i<=n; i++) for (int j=0; j<=M; j++) { B[i][j] = 0; } for (int i = 1; i <= n; i++) { for (int j = 0; j <= M; j++) { B[i][j] = B[i - 1][j]; if ((j >= W[i-1]) && (B[i][j] < B[i - 1][j - W[i - 1]] + V[i - 1])) { B[i][j] = B[i - 1][j - W[i - 1]] + V[i - 1]; } System.out.print(B[i][j] + " "); } System.out.print("\n"); } System.out.println("Max Value:\t" + B[n][M]); System.out.println("Selected Packs: "); while (n != 0) { if (B[n][M] != B[n - 1][M]) { System.out.println("\tPackage " + n + " with W = " + W[n - 1] + " and Value = " + V[n - 1]); M = M - W[n-1]; } n--; } } ``` <figure style="margin-left: auto;margin-right: auto;"> ![](https://img.kancloud.cn/81/ec/81ecff223aca027d375c5bc51e0b2b1a_839x601.png) 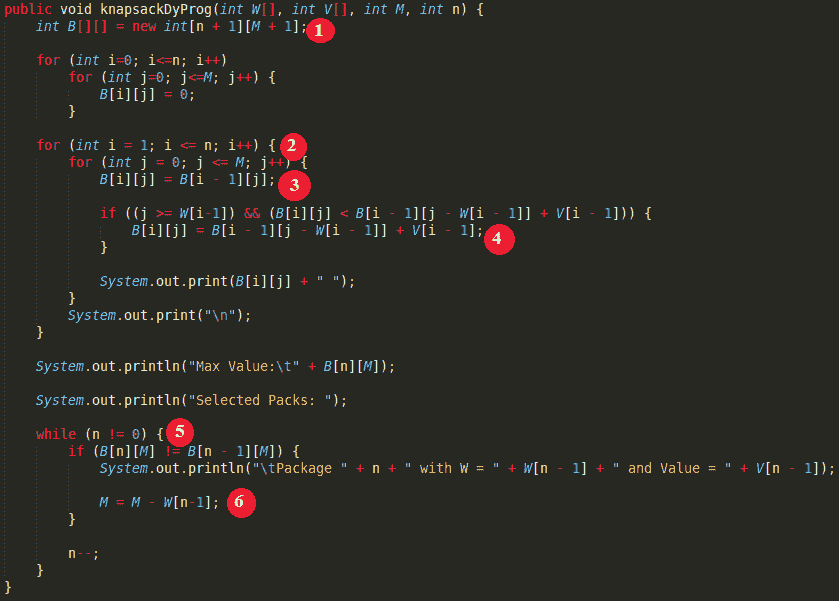Function knapsackDyProg() in Java **代碼說明**： 1. 創建表 B [] []。將每個單元格的默認值設置為 0。 2. 自底向上構建表 B [] []。用檢索公式計算選項表。 3. 計算 B [i] [j]。如果不選擇包 i。 4. 然后評估：如果選擇包 i，則重置 B [i] [j]會更有利。 5. 跟蹤表從第 n 行到第 0 行。 6. 如果選擇包 n。選擇包裝 n 后，只能增加重量 M-W [n-1]。在本教程中，您有兩個示例。這是運行上述程序的 Java 代碼，其中包含兩個示例： ``` public void run() { /* * Pack and Weight - Value */ //int W[] = new int[]{3, 4, 5, 9, 4}; int W[] = new int[]{12, 2, 1, 1, 4}; //int V[] = new int[]{3, 4, 4, 10, 4}; int V[] = new int[]{4, 2, 1, 2, 10}; /* * Max Weight */ //int M = 11; int M = 15; int n = V.length; /* * Run the algorithm */ knapsackDyProg(W, V, M, n); } ``` 您有輸出： * 第一個例子： ``` 0 0 0 3 3 3 3 3 3 3 3 3 0 0 0 3 4 4 4 7 7 7 7 7 0 0 0 3 4 4 4 7 7 8 8 8 0 0 0 3 4 4 4 7 7 10 10 10 0 0 0 3 4 4 4 7 8 10 10 11 Max Value: 11 Selected Packs: Package 5 with W = 4 and Value = 4 Package 2 with W = 4 and Value = 4 Package 1 with W = 3 and Value = 3 ``` * 第二個例子： ``` 0 0 0 0 0 0 0 0 0 0 0 0 4 4 4 4 0 0 2 2 2 2 2 2 2 2 2 2 4 4 6 6 0 1 2 3 3 3 3 3 3 3 3 3 4 5 6 7 0 2 3 4 5 5 5 5 5 5 5 5 5 6 7 8 0 2 3 4 10 12 13 14 15 15 15 15 15 15 15 15 Max Value: 15 Selected Packs: Package 5 with W = 4 and Value = 10 Package 4 with W = 1 and Value = 2 Package 3 with W = 1 and Value = 1 Package 2 with W = 2 and Value = 2 ```